Question

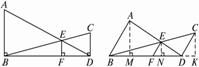
如图1-2-18，△ABC中，D是BC的中点，M是AD上一点，BM、 CM的延长线分别交AC、AB于F、E.求证:EF∥BC.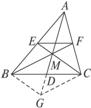

图1-2-18

Answer 1

思路分析:要证明EF∥BC，想通过角之间的关系达到目的显然是不可能的，而要利用成比例线段判定两直线平行的判定定理，图中又没有平行条件，因此要设法作出平行线，以便利用判定定理.作平行线时，要充分考虑到中点D条件的应用.

                 

(1)                      (2)                          (3)

分析一:延长AD至G，使DG=MD，连结BG、CG,如图（1），则四边形BGCM为平行四边形，可以立即将转化成中间比.

解法一:延长AD至G，使DG=MD，连结BG、CG.

∵BD=DC,MD=DG,

∴四边形BGCM为平行四边形.

∴EC∥BG,FB∥CG.

∴=,=.

∴=.∴EF∥BC.

分析二:过A作BC的平行线，与BF、CE的延长线分别交于G、H，如图（2），则

.要证明，只要证AH=AG，这是不难解决的.

解法二:过A作BC的平行线，与BF、CE的延长线分别交于G、H.

∵AH∥DC,AG∥BD,

∴∵BD=DC,∴AH=AG.

∵HG∥BC,∴.

∵AH=AG,∴.∴EF∥BC.

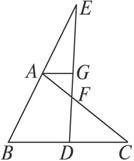
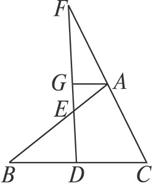
分析三:如图（3），过M作BC的平行线，分别与AB、AC交于G、H，

∵BD=DC,GM=MH.要证EF∥BC，只要证，这可以通过中间比立即证得.

解法三:过M作BC的平行线，分别与AB、AC交于G、H，

则.

∵BD=DC,∴GM=MH.

∵GH∥BC,∵GM=MH,∴∴EF∥BC.