题目内容
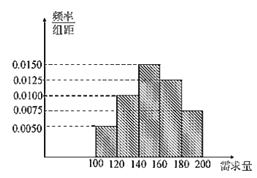
【题目】学校对甲、乙两个班级的同学进行了体能测验，成绩统计如下（每班50人）：
（1）成绩不低于80分记为“优秀”.请填写下面的
列联表，并判断是否有
的把握认为“成绩优秀”与所在教学班级有关？
（2）从两个班级的成绩在
的所有学生中任选2人，其中，甲班被选出的学生数记为
，求的分布列与数学期望.
赋：
.
【答案】(1)列联表见解析，有
的把握认为：“成绩优秀”与所在教学班级有关.
(2) 
的分布列见解析，
.
【解析】
（1）根据数据对应填写表格，根据公式求卡方，对照参考数据确定把握率，（2）先确定随机变量取法，再根据组合数求对应概率，列表可得分布列，最后根据数学期望公式求期望.
（1）
列联表如下：
所以有的把握认为：“成绩优秀”与所在教学班级有关.
（2）由已知，甲、乙两个班级成绩在
的学生数分别为6人，8人
的取值为0，1，2
，
，
的分布列：
的数学期望：
.
练习册系列答案
相关题目
【题目】以下表格记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊，无法确认，在图中以
表示.
甲组 | 9 | 9 | 11 | 11 |
乙组 |
| 8 | 9 | 10 |
（1）如果
，求乙组同学植树棵数的平均数和方差；
（2）如果
，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率.
