Question

已知F₁，F₂分别是双曲线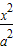-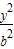=1（a＞b＞0）的两个焦点，A和B是以O（O为坐标原点）为圆心，|OF₁|为半径的圆与该双曲线左支的两个交点，且△F₂AB是等边三角形，则双曲线的离心率为（ ）
A．
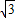
B．
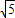
C．
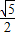
D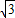．+1

Answer 1

【答案】分析：先设F₁F₂=2c，根据△F₂AB是等边三角形，判断出∠AF₂F₁=30°，进而在RT△AF₁F₂中求得AF₁和AF₂，进而根据栓曲线的简单性质求得a，则双曲线的离心率可得．
解答：解：如图，设F₁F₂=2c，
∵△F₂AB是等边三角形，
∴∠AF₂F₁=30°，
∴AF₁=c，AF₂=C，
∴a=
e==+1，
故选D
点评：本题主要考查了双曲线的简单性质．考查了学生综合分析问题和数形结合的思想的运用．属基础题．