题目内容
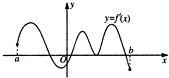函数f（x）的定义域为开区间（a，b），其导函数在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内极大值点有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
考点：利用导数研究函数的极值
专题：计算题,导数的综合应用
分析：根据运用导数判断极值的方法：考虑导数与x轴的交点的左右两侧导数的变化，找左正右负的．
解答：
解：由导函数的图象可知，在（a，b）内，与x轴有四个交点，第一个点处导数左正右负，第二个点处导数左负右正，第三个点处导数左正右正，第四个点处导数左正右负，则函数f（x）在开区间（a，b）内极大值点有2个．
故选：B．
故选：B．
点评：本题考查导数的运用：判断极值，注意图象与x轴的交点的左右两侧导数的变化，属于基础题．
练习册系列答案
相关题目
在复平面内，复数z=i（1-i）（i是虚数单位）对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合M={x|0≤x＜2}，N={x|x2-2x-1＜0}，则集合M∩N=（ ）
| A、{x|0≤x＜1} |
| B、{x|0≤x≤1} |
| C、{x|0≤x＜2} |
| D、{ x|0≤x≤2 } |
已知3-
i=z（-2+
i），那么复数z在平面内对应的点位于（ ）
| 3 |
| 3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
用反证法证明“如果a＞b，那么
＞
”这个命题时，第一步应作的假设为（ ）
| 3 | a |
| 3 | b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
以原点为角的顶点，x轴正方向为角的始边，终边在x轴上的角等于（ ）
| A、0°、90°或270° |
| B、k•360°（k∈Z） |
| C、k•180°（k∈Z） |
| D、k•90°（k∈Z） |
函数f（x）=
，则f（-2）等于（ ）
|
|
| A、1 | B、2 | C、3 | D、4 |