题目内容
三棱锥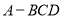 中,
中,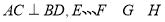 分别是
分别是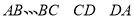 的中点,则四边形
的中点,则四边形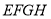 是( )
是( )
A.菱形 B.矩形 C.梯形 D.正方形
B
【解析】
试题分析:如图,在 中,点
中,点 分别为边
分别为边 的中点,所以
的中点,所以 ,同理
,同理 ,所以
,所以 ,
, ,所以四边形
,所以四边形 为平行四边形,而
为平行四边形,而 ,所以
,所以 ,所以四边形
,所以四边形 是矩形,故选B.
是矩形,故选B.

考点:空间中的平行与垂直关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
三棱锥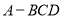 中,
中,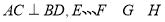 分别是
分别是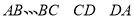 的中点,则四边形
的中点,则四边形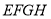 是( )
是( )
A.菱形 B.矩形 C.梯形 D.正方形
B
【解析】
试题分析:如图,在 中,点
中,点 分别为边
分别为边 的中点,所以
的中点,所以 ,同理
,同理 ,所以
,所以 ,
, ,所以四边形
,所以四边形 为平行四边形,而
为平行四边形,而 ,所以
,所以 ,所以四边形
,所以四边形 是矩形,故选B.
是矩形,故选B.

考点:空间中的平行与垂直关系.

 阅读快车系列答案
阅读快车系列答案