题目内容
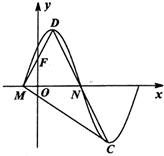 (2012•温州二模)如图是函数f(x)=Asin(ωx+φ),A>0,ω>0,0<φ<
(2012•温州二模)如图是函数f(x)=Asin(ωx+φ),A>0,ω>0,0<φ<| π |
| 2 |
| 2π |
| 3 |
(I)求函数f(x)的解析式;
(II)在△CDM中,记∠DMN=α,∠CMN=β.证明:sinC=2cosαsinβ.
分析:(I)先由条件得到A=2,再由 S△DMN=
S△CDM=
=
,求得 T=
=
,从而求得ω=3.求出点M的坐标为(-
,0),由五点法作图求得φ 值.
(II)在△CDM中,由题意可得 tanα=3tanβ,即 sinαcosβ=3cosαsinβ.而DC=2DM,故sinC=
sin∠DMC=
sin(α+β),化简可得sinC=2cosαsinβ成立.
| 1 |
| 2 |
| T•A |
| 4 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| ω |
| π |
| 12 |
(II)在△CDM中,由题意可得 tanα=3tanβ,即 sinαcosβ=3cosαsinβ.而DC=2DM,故sinC=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(I)由已知 点F (0,1)是线段MD的中点知A=2,∵S△DMN =
S△CDM=
MN•A=
=
,∴T=
=
,ω=3.
∴函数f(x)=2sin(3x+φ),再由已知可得点M的坐标为(-
,0),由五点法作图可得 3(-
)+φ=0,∴φ=
.
(II)在△CDM中,∠DMN=α,∠CMN=β,则有 tanα=3tanβ,即 sinαcosβ=3cosαsinβ.
而DC=2DM,故sinC=
sin∠DMC=
sin(α+β)=
sinαcosβ+
cosαsinβ=
cosαsinβ+
cosαsinβ=2cosαsinβ,
∴sinC=2cosαsinβ成立.
| 1 |
| 2 |
| 1 |
| 2 |
| T•A |
| 4 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| ω |
∴函数f(x)=2sin(3x+φ),再由已知可得点M的坐标为(-
| π |
| 12 |
| π |
| 12 |
| π |
| 4 |
(II)在△CDM中,∠DMN=α,∠CMN=β,则有 tanα=3tanβ,即 sinαcosβ=3cosαsinβ.
而DC=2DM,故sinC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴sinC=2cosαsinβ成立.
点评:本题主要考查利用y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,三角函数的恒等变换及化简求值,属于中档题.

练习册系列答案
相关题目
 (2012•温州二模)某程序框图如图所示,该程序运行后输出的S的值是( )
(2012•温州二模)某程序框图如图所示,该程序运行后输出的S的值是( )