题目内容

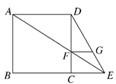精英家教网已知：如图，四边形ABCD是正方形，延长BC到点E，连接AE交CD于F，FG∥AD交DE于G．求证：FC=FG．
分析：根据两条直线AB∥CD，写出对应线段成比例，根据FG∥AD，得到比例式，两个比例式中有共同的式子，根据等量代换，得到比例式，根据比例式中分子相同，得到分母相同，结论得证．
解答：证明：在正方形ABCD中，
AB∥CD，
∴
CF
AB
=
EF
AE
．
∵FG∥AD，
∴
FG
AD
=
EF
AE
．
∴
CF
AB
=
FG
AD
．
∵AB=AD，
∴CF=FG．
点评：本题考查平行线分线段成比例定理，考查等量代换，是一个基础题，这种题目可以单独出现，也可以出现在解答题目的一问中．
练习册系列答案
相关题目
精英家教网
如图，四边形OABC为矩形，点A、C的坐标分别为（a+1，0）（a＞1）、（0，1），点D在OA上，坐标为（a，0），椭圆C分别以OD、OC为长、短半轴，CD是椭圆在矩形内部的椭圆弧．已知直线l：y=-x+m与椭圆弧相切，且与AD相交于点E．
（Ⅰ）当m=2时，求椭圆C的标准方程；
（Ⅱ）圆M在矩形内部，且与l和线段EA都相切，若直线l将矩形OABC分成面积相等的两部分，求圆M面积的最大值．
如图，四边形ABCD中，△BCD为正三角形，AD=AB=2，BD=2
3
，AC与BD交于O点．将△ACD沿边AC折起，使D点至P点，已知PO与平面ABCD所成的角为θ，且P点在平面ABCD内的射影落在△ACD内．
（Ⅰ）求证：AC⊥平面PBD；
（Ⅱ）若已知二面角A-PB-D的余弦值为
21
7
，求θ的大小．
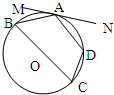A．已知方程|2x-1|-|2x+1|=a+1有实数解，则a的取值范围为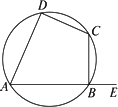
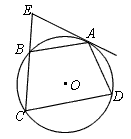
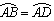[-3，-1）
[-3，-1）
．
B．如图，四边形ABCD内接于⊙O，BC是直径，MN切⊙O于A，∠MAB=25•，则∠D=
115°
115°
．
C．设曲线C的参数方程为
x=2+3cosθ
y=-1+3sinθ
（θ为参数），直线l的参数方程为
x=1+2t
y=1+t
（t为参数），则直线l被曲线C截得的弦长为
4
4
．

圆内接四边形判定定理的推论的证明．.

已知：如图，四边形ABCD，延长AB到E，∠EBC＝∠CDA．

求证：A、B、C、D四点共圆．
已知：如图，四边形ABCD内接于⊙O，，过A点的切线交CB的延长线于E点，求证：AB2=BE·CD。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网