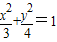Question

已知椭圆两个焦点的坐标分别为，，并且经过点．过左焦点，斜率为的直线与椭圆交于，两点． 设，延长，分别与椭圆交于两点．

（I）求椭圆的标准方程；   （II）若点，求点的坐标；

（III）设直线的斜率为，求证：为定值．

 

 

Answer 1

【答案】

解：（I）因为椭圆的焦点在轴上，所以设它的标准方程为，

由椭圆的定义知,

.  ----------------2分

所以，,

所以所求椭圆的标准方程为.  ---------------4分

（II）直线的方程为，

代入椭圆方程，得

解得（舍），或.    --------------6分

代入直线的方程，得，

所以点的坐标为.  ---------------7分

（III）设，，，，

直线的方程为，所以.

代入椭圆方程，消去得：

.   --------------8分

又因为点在椭圆上，有

方程化简为.     -----------------9分

则，且，所以.

代入直线的方程，得，所以 .  -------------10分

同理，

.  ------------------12分

因为三点共线，所以.

即.  --------------------13分

所以，而.

所以为定值.  -------------------14分

 

【解析】略