题目内容

已知（x-1）（x+1）9=a0+a1x+a2x2+…+a9x9+a10x10，则a2+a4+a6+a8+a10=（　　）
分析：分别令x=0，求a0，令x=1，求a0+a1+a2+…+a9+a10；令x=-1，求a0-a1+a2+…-a9+a10，从而有a0+a2+a4+a6+a8+a10=0，故可求a2+a4+a6+a8+a10．
解答：解：令x=0，则a0=-1，令x=1，则a0+a1+a2+…+a9+a10=0；令x=-1，则a0-a1+a2+…-a9+a10=0，∴a0+a2+a4+a6+a8+a10=0，
∴a2+a4+a6+a8+a10=1，
故选C．
点评：本题考查通过赋值求常数项、通过赋值求展开式的系数和．
练习册系列答案
相关题目
（1）求证：函数f（x）=x+
a
x
是奇函数；
（2）已知函数g（x）=x+
1
x
在区间（0，1）上是单调减函数，在区间（1，+∞）上是单调增函数；函数g（x）=x+
4
x
在区间（0，2）上是单调减函数，在区间（2，+∞）上是单调增函数；猜想出函数g（x）=x+
b2
x
，（b＞0），x∈（0，+∞）的单调区间；
（3）指出函数h（x）=x+
8
x
，x∈（-∞，0）在什么时候取最大值，最大值是多少．
（2006•崇文区二模）已知A={x|x＜1}，B={x|（x-2）•（x-1）≤0}，则A∪B=（　　）
已知f(x)是定义在R上的函数．f(1)=1，且对于任意的xÎR，都有f(x+5)³f(x)+5，f(x+1)£f(x)+1，若g(x)=f(x)+1-x，则g（2001）=________．
（1）求证：函数f（x）=x+
a
x
是奇函数；
（2）已知函数g（x）=x+
1
x
在区间（0，1）上是单调减函数，在区间（1，+∞）上是单调增函数；函数g（x）=x+
4
x
在区间（0，2）上是单调减函数，在区间（2，+∞）上是单调增函数；猜想出函数g（x）=x+
b2
x
，（b＞0），x∈（0，+∞）的单调区间；
（3）指出函数h（x）=x+
8
x
，x∈（-∞，0）在什么时候取最大值，最大值是多少．
已知函数f（x）=x2+bsinx-2（b∈R），F（x）=f（x）+2，且对于任意实数x，恒有F（x-5）=F（5-x），
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）已知函数g（x）=f（x）+2（x+1）+ alnx在区间（0，1）上单调，求实数a的取值范围；
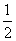（Ⅲ）函数h（x）=2lnx-f（x）-k有几个零点？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网