题目内容
若不等式 ≥
≥ 对任意的正数x,y总成立,则实数k的取值范围________.
对任意的正数x,y总成立,则实数k的取值范围________.
k≥ 或k<0
或k<0
分析:若k>0,由题意可得k应大于或等于 的最大值,由基本不等式可得
的最大值,由基本不等式可得 的最大值为
的最大值为 ,故k≥
,故k≥ ,当k<0 时,不等式显然成立,从而得到答案.
,当k<0 时,不等式显然成立,从而得到答案.
解答:若k>0,由于不等式 ≥
≥ 对任意的正数x,y总成立,∴k≥
对任意的正数x,y总成立,∴k≥ ,
,
故k应大于或等于 的最大值.∵
的最大值.∵ ≤
≤ =
= =
= ,
,
故 的最大值为
的最大值为 ,故k≥
,故k≥ .
.
当k<0 时,不等式显然成立.综上,k≥ 或k<0,
或k<0,
故答案为k≥ 或k<0.
或k<0.
点评:本题考查函数的恒成立问题,基本不等式的应用,体现了分类讨论的数学思想,注意容易忽视k<0 时的情况.
 或k<0
或k<0分析:若k>0,由题意可得k应大于或等于
 的最大值,由基本不等式可得
的最大值,由基本不等式可得 的最大值为
的最大值为 ,故k≥
,故k≥ ,当k<0 时,不等式显然成立,从而得到答案.
,当k<0 时,不等式显然成立,从而得到答案.解答:若k>0,由于不等式
 ≥
≥ 对任意的正数x,y总成立,∴k≥
对任意的正数x,y总成立,∴k≥ ,
,故k应大于或等于
 的最大值.∵
的最大值.∵ ≤
≤ =
= =
= ,
,故
 的最大值为
的最大值为 ,故k≥
,故k≥ .
.当k<0 时,不等式显然成立.综上,k≥
 或k<0,
或k<0,故答案为k≥
 或k<0.
或k<0.点评:本题考查函数的恒成立问题,基本不等式的应用,体现了分类讨论的数学思想,注意容易忽视k<0 时的情况.

练习册系列答案
相关题目
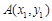 、
、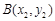 是函数
是函数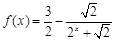 图象上任意两点,且
图象上任意两点,且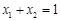 .
.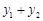 的值;
的值;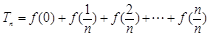 (其中
(其中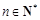 ),求
),求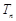 ;
;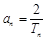 (
(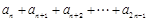 >
>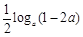 对任意的正整数n恒成立,求实数a的取值范围.
对任意的正整数n恒成立,求实数a的取值范围. 
 (提示 :
(提示 : )
) 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数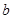 的取值范围;
的取值范围;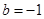 ,证明对任意的正整数n,不等式
,证明对任意的正整数n,不等式 都成立.
都成立. ≥
≥ ,对任意的正实数
,对任意的正实数 总成立,则正实数
总成立,则正实数 的取值范围为: ▲ .
的取值范围为: ▲ .