题目内容
1.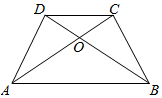 如图.在四边形ABCD中,$\overrightarrow{AB}$=2$\overrightarrow{DC}$,O在线段AC上,且AO:OC=2:1,试判断B,O,D三点是否在同一条直线上.
如图.在四边形ABCD中,$\overrightarrow{AB}$=2$\overrightarrow{DC}$,O在线段AC上,且AO:OC=2:1,试判断B,O,D三点是否在同一条直线上.
分析 $\overrightarrow{AB}$=2$\overrightarrow{DC}$,可得AB∥DC,$\frac{AB}{DC}$=2.设BD与AC相交于点O′.利用平行线的性质可证:点O与O′重合.
解答 解:∵$\overrightarrow{AB}$=2$\overrightarrow{DC}$,
∴AB∥DC,$\frac{AB}{DC}$=2.
设BD与AC相交于点O′.
则$\frac{B{O}^{′}}{D{O}^{′}}=\frac{A{O}^{′}}{C{O}^{′}}=\frac{AB}{DC}$=$\frac{2}{1}$
∵O在线段AC上,且AO:OC=2:1,
∴点O与O′重合.
因此B,O,D三点在同一条直线上.
点评 本题考查了向量共线定理、平行线的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.函数f(x)=ex+2x-3的零点所在区间是( )
| A. | (-2,-1) | B. | (-1,0) | C. | (1,2) | D. | (0,1) |
12.sin80°sin40°-cos80°cos40°的值为( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
6.命题p:x>4是命题q:x-4>m的充要条件,则m的取值范围是( )
| A. | m>0 | B. | m<0 | C. | m=0 | D. | m≥0 |
2.若不等式ax2+5x-2>0的解集是{x|$\frac{1}{2}$<x<2},则a的值为( )
| A. | -$\frac{3}{2}$ | B. | 2 | C. | -2 | D. | $\frac{1}{2}$ |
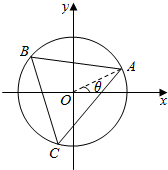 如图,正三角形ABC内接于单位圆O,设∠AOx=θ,A(xA,yA),B(xB,yB),C(xC.yC).
如图,正三角形ABC内接于单位圆O,设∠AOx=θ,A(xA,yA),B(xB,yB),C(xC.yC).