题目内容
已知等差数列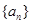 的前
的前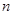 项和为
项和为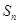 ,公差
,公差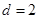 ,且
,且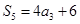 .
.
(1)求数列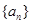 的通项公式;
的通项公式;
(2)设数列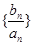 是首项为1,公比为
是首项为1,公比为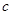 的等比数列,求数列
的等比数列,求数列 的前n项和
的前n项和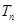 .
.
(1)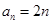 (2)
(2) 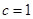 时,
时,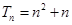 ;
;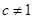 时,
时,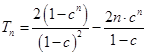
解析试题分析:(1)将已知条件 中的
中的 均用
均用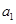 表示,即可解得
表示,即可解得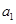 的值。再根据等差的通项公式求其通项公式即可。(2)根据等比数列的通项公式可得
的值。再根据等差的通项公式求其通项公式即可。(2)根据等比数列的通项公式可得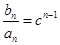 ,即可得
,即可得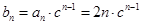 (注意对公比
(注意对公比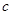 是否为1进行讨论)。当
是否为1进行讨论)。当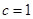 时,
时,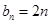 ,根据等差数列前
,根据等差数列前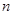 项和公式求
项和公式求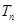 ;当
;当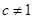 时,
时,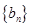 的通项公式等于等差乘等比的形式,故应用错位相减法求其前n项和
的通项公式等于等差乘等比的形式,故应用错位相减法求其前n项和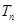 。
。
解:(1)因为公差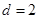 ,且
,且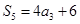 ,
,
所以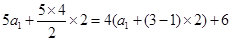 . 2分
. 2分
所以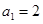 . 4分
. 4分
所以等差数列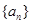 的通项公式为
的通项公式为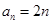 . 5分
. 5分
(2)因为数列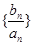 是首项为1,公比为
是首项为1,公比为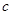 的等比数列,
的等比数列,
所以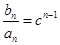 . 6分
. 6分
所以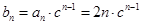 . 7分
. 7分
(1)当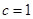 时,
时,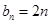 . 8分
. 8分
所以 . 9分
. 9分
(2)当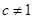 时,
时,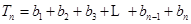
因为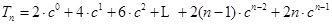 ① 9分
① 9分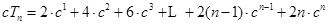 ② 10分
② 10分
①-②得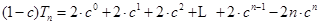 11分
11分
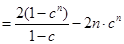 12分
12分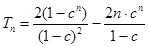 13分
13分
考点:1等差数列的通项公式、前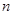 项和公式;2错位相减法求数列前
项和公式;2错位相减法求数列前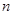 项和。
项和。

练习册系列答案
相关题目
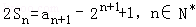 ,且a1,a2+5,a3成等差数列.
,且a1,a2+5,a3成等差数列.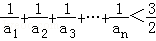 .
.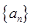 中,
中,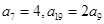 .
.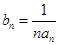 ,求数列
,求数列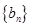 的前
的前 项和
项和 .
.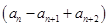 x+an+1cos x-an+2sin x满足f′
x+an+1cos x-an+2sin x满足f′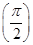 =0.
=0.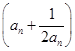 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.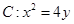 ,直线
,直线 过抛物线
过抛物线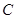 的焦点
的焦点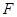 ,交
,交 轴于点
轴于点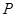 .
.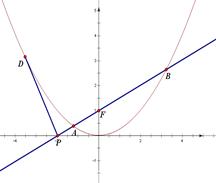
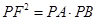 ;
;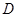 (异于原点),
(异于原点),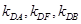 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;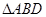 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.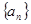 是等差数列,且
是等差数列,且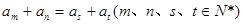 ,
,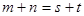 ;
;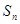 是等差数列
是等差数列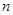 项的和,则
项的和,则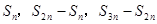 成等差数列;
成等差数列;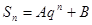 ;(其中
;(其中 是非零常数,
是非零常数,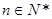 ),则
),则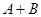 为零.
为零.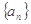 ,等比数列
,等比数列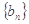 ,满足
,满足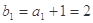 ,
,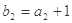 ,
,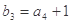 .
.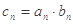 ,求数列{
,求数列{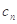 }的前n项和.
}的前n项和.