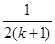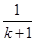题目内容
用数学归纳法证明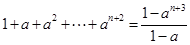 (
(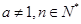 ),在验证当n=1时,等式左边应为
),在验证当n=1时,等式左边应为
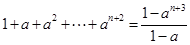 (
(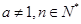 ),在验证当n=1时,等式左边应为
),在验证当n=1时,等式左边应为| A.1 | B.1+a | C.1+a+a2 | D.1+a+a2+a3 |
D
试题分析:注意到
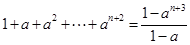 的左端,表示
的左端,表示 直到
直到 共n+3项的和,所以,当n=1时,等式左边应为1+a+a2+a3,选D。
共n+3项的和,所以,当n=1时,等式左边应为1+a+a2+a3,选D。点评:简单题,应用数学归纳法证明问题,应遵循“两步一结”。对于,n=1的情况,注意明确“项数”。

练习册系列答案
相关题目
 在点
在点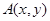 处的切线斜率为
处的切线斜率为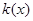 ,且
,且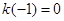 .对一切实数
.对一切实数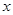 ,不等式
,不等式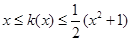 恒成立(
恒成立(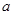 ≠0).
≠0).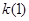 的值;
的值;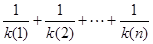 >
>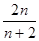 .
.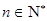 时,
时,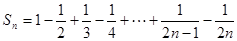
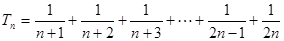
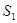 ,
,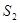 ,
,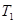 ,
,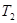 ;
;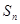 与
与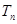 的关系,并用数学归纳法证明.
的关系,并用数学归纳法证明.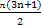 (n∈N*)的第二步中,当n=k+1时等式左边与n=k时的等式左边的差等于 .
(n∈N*)的第二步中,当n=k+1时等式左边与n=k时的等式左边的差等于 .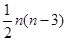 条时,第一步检验n等于( )
条时,第一步检验n等于( )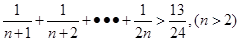 ”的过程中,由n=k到n=k+1时,不等式的左边( )
”的过程中,由n=k到n=k+1时,不等式的左边( )