题目内容
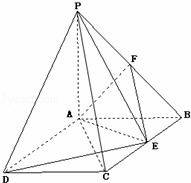
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(Ⅰ)求三棱锥E﹣PAD的体积;
(Ⅱ)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅲ)证明:无论点E在边BC的何处,都有PE⊥AF.
考点:
直线与平面平行的判定;棱柱、棱锥、棱台的体积;直线与平面垂直的性质.
分析:
本题考查了空间几何体的体积、线面位置关系的判定、线面垂直等知识点,
(Ⅰ)利用换底法求VP﹣ADE即可;(Ⅱ)利用三角形的中位线及线面平行的判定定理解决;
(Ⅲ)通过证明AF⊥平面PBE即可解决.
解答:
解:(Ⅰ)三棱锥E﹣PAD的体积![]() .(4分)
.(4分)
(Ⅱ)当点E为BC的中点时,EF与平面PAC平行.(5分)
∵在△PBC中,E、F分别为BC、PB的中点,
∴EF∥PC,又EF⊄平面PAC,而PC⊂平面PAC,
∴EF∥平面PAC.(8分)
(Ⅲ)证明:
∵PA⊥平面ABCD,BE⊂平面ABCD,
∴EB⊥PA,又EB⊥AB,AB∩AP=A,AB,AP⊂平面PAB,
∴EB⊥平面PAB,又AF⊂平面PAB,
∴AF⊥BE.(10分)
又PA=AB=1,点F是PB的中点,
∴AF⊥PB,
又∵PB∩BE=B,PB,BE⊂平面PBE,
∴AF⊥平面PBE.
∵PE⊂平面PBE,
∴AF⊥PE.(12分)
点评:
无论是线面平行(垂直)还是面面平行(垂直),都源自于线与线的平行(垂直),这种“高维”向“低维”转化的思想方法,在解题时非常重要,在处理实际问题的过程中,可以先从题设条件入手,分析已有的平行(垂直)关系,再从结论入手分析所要证明的平行(垂直)关系,从而架起已知与未知之间的桥梁.

练习册系列答案
相关题目
 如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点. 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 如图,PA⊥平面ABC,AC⊥BC,AB=2,
如图,PA⊥平面ABC,AC⊥BC,AB=2, (2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点
(2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.