题目内容
直线l1:x+3y-7=0,l2:kx+y-2=0与x,y轴的正半轴所围成的四边形有外接圆,则k等于 .
【答案】分析:四边形有外接圆,则对角互补,由于x轴与y轴垂直,所以直线l1:x+3y-7=0,l2:kx+y-2=0互相垂直,利用两直线垂直的充要条件,即可解得k的值
解答:解:∵直线l1:x+3y-7=0,l2:kx+y-2=0与x,y轴的正半轴所围成的四边形有外接圆
而x轴与y轴垂直,
∴直线l1:x+3y-7=0,l2:kx+y-2=0互相垂直
∴1×k+3×1=0
∴k=-3
故答案为-3
点评:本题主要考查了两条直线的位置关系,两直线垂直的充要条件,四点共圆的性质等基础知识,发现两直线垂直是解决本题的关键
解答:解:∵直线l1:x+3y-7=0,l2:kx+y-2=0与x,y轴的正半轴所围成的四边形有外接圆
而x轴与y轴垂直,
∴直线l1:x+3y-7=0,l2:kx+y-2=0互相垂直
∴1×k+3×1=0
∴k=-3
故答案为-3
点评:本题主要考查了两条直线的位置关系,两直线垂直的充要条件,四点共圆的性质等基础知识,发现两直线垂直是解决本题的关键

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
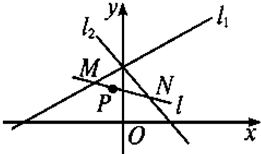 如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.
如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.