题目内容
已知椭圆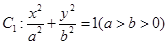 的长轴长为
的长轴长为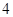 ,离心率为
,离心率为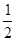 ,
,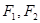 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点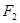 ,且与直线
,且与直线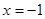 相切.
相切.
(1)求椭圆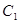 及动圆圆心轨迹
及动圆圆心轨迹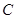 的方程;
的方程;
(2) 在曲线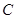 上有两点
上有两点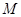 、
、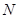 ,椭圆
,椭圆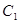 上有两点
上有两点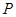 、
、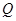 ,满足
,满足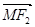 与
与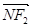 共线,
共线,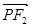 与
与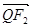 共线,且
共线,且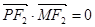 ,求四边形
,求四边形 面积的最小值.
面积的最小值.
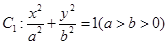 的长轴长为
的长轴长为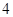 ,离心率为
,离心率为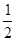 ,
,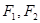 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点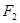 ,且与直线
,且与直线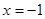 相切.
相切.(1)求椭圆
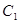 及动圆圆心轨迹
及动圆圆心轨迹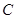 的方程;
的方程;(2) 在曲线
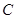 上有两点
上有两点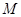 、
、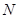 ,椭圆
,椭圆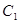 上有两点
上有两点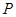 、
、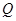 ,满足
,满足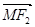 与
与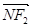 共线,
共线,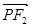 与
与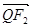 共线,且
共线,且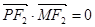 ,求四边形
,求四边形 面积的最小值.
面积的最小值.(1)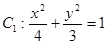 ,
,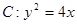
(2)四边形PMQN面积的最小值为8
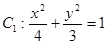 ,
,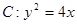
(2)四边形PMQN面积的最小值为8
试题分析:解:(1)(ⅰ)由已知可得
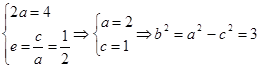 ,
,则所求椭圆方程
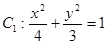 . 3分
. 3分(ⅱ)由已知可得动圆圆心轨迹为抛物线,且抛物线
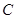 的焦点为
的焦点为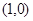 ,准线方程为
,准线方程为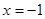 ,则动圆圆心轨迹方程为
,则动圆圆心轨迹方程为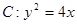 . 5分
. 5分(2)当直线MN的斜率不存在时,
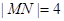 ,此时PQ的长即为椭圆长轴长,
,此时PQ的长即为椭圆长轴长,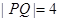
从而
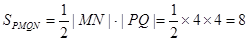 6分
6分设直线MN的斜率为k,则k≠0,直线MN的方程为:
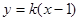 ,
,直线PQ的方程为

设
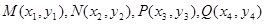
由
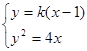 ,消去
,消去 可得
可得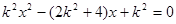 ---8分
---8分由抛物线定义可知:
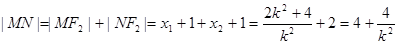 9分
9分由
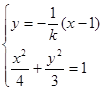 消去
消去 得
得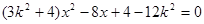 ,
,从而
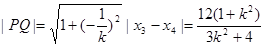 10分
10分∴
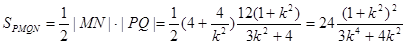
令
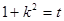 ,∵
,∵ 则
则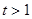
则
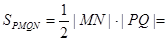
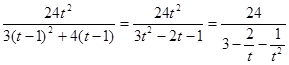
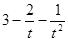 =
= ,所以
,所以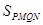 =
=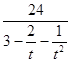 >8 11分
>8 11分所以四边形PMQN面积的最小值为8 12分
点评:主要是考查了轨迹方程的求解,以及联立方程组结合韦达定理来求解面积,属于基础题。

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
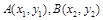 是椭圆
是椭圆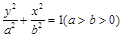 上的两点,已知向量
上的两点,已知向量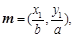
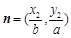 ,若
,若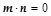 且椭圆的离心率
且椭圆的离心率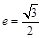 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.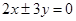 为渐近线,且经过点
为渐近线,且经过点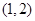 的双曲线标准方程是
的双曲线标准方程是 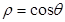 和参数方程
和参数方程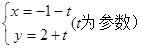 所表示的图形分别是( )
所表示的图形分别是( ) (
( >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
 ,
, 为双曲线
为双曲线 的右焦点,点
的右焦点,点 ,
, 为
为 轴正半轴上的动点。
轴正半轴上的动点。 的最大值为( )
的最大值为( )



 与曲线
与曲线 的交点个数为( )
的交点个数为( )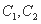 都是以原点O为对称中心、坐标轴为对称轴、离心率相等的椭圆.点M的坐标是(0,1),线段MN是曲线
都是以原点O为对称中心、坐标轴为对称轴、离心率相等的椭圆.点M的坐标是(0,1),线段MN是曲线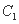 的短轴,并且是曲线
的短轴,并且是曲线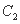 的长轴 . 直线
的长轴 . 直线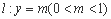 与曲线
与曲线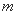 =
=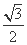 ,
,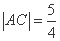 时,求椭圆
时,求椭圆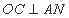 ,求
,求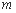 的值.
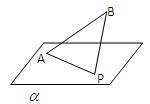
的值.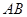 是平面
是平面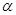 的斜线段,
的斜线段,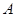 为斜足。若点
为斜足。若点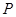 在平面
在平面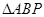 的面积为定值,则动点
的面积为定值,则动点