Question

函数f（x）=

sinx，sinx≤cosx cosx，sinx＞cosx

，则函数图象的对称轴方程是

x=

π

4

+kπ（k∈Z）

．

Answer 1

分析：根据题意，函数f（x）的图象在正弦曲线、余弦曲线中选取纵坐标较小的点而构成．由此化简函数解析式，并在同一坐标系内作出正余弦曲线，得到f（x）的图象并加以观察，可得当sinx=cosx时经过相应的点作x轴的垂线，即可得到函数图象的一条对称轴，进而可得函数f（x）图象的对称轴方程．

解答：解：根据题意，可得
当sinx≤cosx时，即x∈[-

3π

4

+2kπ，

π

4

+2kπ]（k∈Z）时，f（x）=sinx；
当sinx＞cosx时，即x∈[

π

4

+2kπ，

5π

4

+2kπ]（k∈Z）时，f（x）=cosx．
∴f（x）=

sinx     x∈[- 3π 4 +2kπ， π 4 +2kπ]，              cosx    x∈[ π 4 +2kπ， 5π 4 +2kπ]

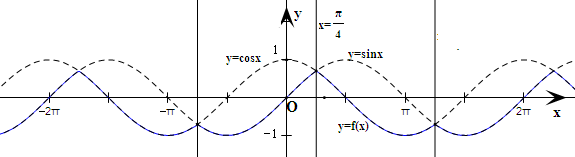
因此作出函数的图象并加以观察，可得当sinx=cosx时，经过相应的点作x轴的垂线，
即可得到函数图象的一条对称轴，此时x=

π

4

+kπ，（k∈Z）．
∴函数图象的对称轴方程是x=

π

4

+kπ（k∈Z）．
故答案为：x=

π

4

+kπ（k∈Z）．

点评：本题以正余弦曲线为载体，求函数f（x）图象的对称轴方程．着重考查了正余弦函数的图象与性质、简单的三角方程与函数图象的对称性等知识，属于中档题．