题目内容
15. 如图,已知在侧棱垂直于底面三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,已知在侧棱垂直于底面三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.(Ⅰ)求证:AC1∥平面CDB1;
(Ⅱ)求三棱锥A1-B1CD的体积.
分析 (I)设BC1与CB1的交点坐标为O,连结OD,利用中位线定理可得OD∥AC1,故而AC1∥平面CDB1;
(II)求出C到AB的距离即为C到平面ABB1A1的距离,代入棱锥的体积公式即可.
解答 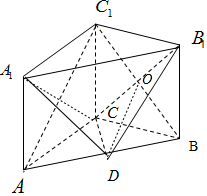 (I)证明:设BC1与CB1的交点坐标为O,连结OD,
(I)证明:设BC1与CB1的交点坐标为O,连结OD,
∵四边形BCC1B1是平行四边形,
∴O是BC1的中点,又D是AB的中点,
∴OD∥AC1,
又OD?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
(II)解:在Rt△ABC中,C到AB的距离h=$\frac{AC•BC}{AB}$=$\frac{12}{5}$,
又平面ABC⊥平面ABB1A1,
∴C到平面ABB1A1的距离为h=$\frac{12}{5}$.
∴V${\;}_{{A}_{1}-{B}_{1}CD}$=$\frac{1}{3}$S${\;}_{△{A}_{1}{B}_{1}D}$•h=$\frac{1}{3}×5×4×\frac{12}{5}$=16.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
5.在三角形△ABC中,a,b,c分别是内角A,B,C的对边,2bsinB=(2a+c)sinA+(2c+a)sinC.
(Ⅰ)求B的大小;
(Ⅱ)当b=4$\sqrt{2}$,a=c,求此三角形的面积.
(Ⅰ)求B的大小;
(Ⅱ)当b=4$\sqrt{2}$,a=c,求此三角形的面积.
3.椭圆$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{25}$=1上一点到两个焦点的距离之和为( )
| A. | 2$\sqrt{10}$ | B. | 2$\sqrt{15}$ | C. | 5 | D. | 10 |
10.双曲线$\frac{{x}^{2}}{m}$-y2=1(m>0)的实轴长为6,则m等于( )
| A. | 3 | B. | 6 | C. | 9 | D. | 36 |
20.已知直线ax+2y+2=0与直线3x+4y+1=0互相垂直,则a的值为( )
| A. | -$\frac{8}{3}$ | B. | -$\frac{3}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{8}{3}$ |
7.设f(x)=$\left\{\begin{array}{l}{{e}^{x}(x≤0)}\\{lnx(x>0)}\end{array}\right.$,则f(f($\frac{1}{2}$))=( )
| A. | $\sqrt{e}$ | B. | ln$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
 如图所示,等腰梯形ABCD的点C,D为半圆上的动点,CD∥AB,底边AB为圆O的直径,∠BOC=θ,OB=1.设等腰梯形ABCD的周长为y.
如图所示,等腰梯形ABCD的点C,D为半圆上的动点,CD∥AB,底边AB为圆O的直径,∠BOC=θ,OB=1.设等腰梯形ABCD的周长为y.