Question

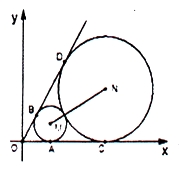
【题目】如图，已知圆心坐标为的圆与轴及直线分别相切于、两点，另一圆与圆外切，且与轴及直线分别相切于、两点．

（1）求圆和圆的方程；

（2）过点作直线的平行线，求直线被圆截得的弦的长度．

Answer 1

【答案】（1），；（2）．

【解析】

试题分析：（1）圆的圆心已知，且其与轴及直线分别相切于两点，故半径易知，另一圆与圆外切、且与轴及直线分别相切于两点，由相似性易得其圆心坐标与半径，依定义写出两圆的方程即可；（2）由于点位置不特殊，可以由对称性转化为求过点且与线平行的线被圆截得弦的长度．

试题解析：（1）由于与的两边均相切，故到及的距离均为的半径，则在的平分线上，同理，也在的平分线上，

即三点共线，且为的平分线，

∵的坐标为，∴到轴的距离为1，即的半径为1，

则的方程为，

设的半径为，其与轴的切点为，连接、，

由可知，，

即．

则，则圆的方程为；

（2）由对称性可知，所求的弦长等于过点，直线的平行线被圆截得的弦的长度，

此弦的方程是，即：，

圆心到该直线的距离，则弦长=．