题目内容
如图，O为原点，从椭圆| x2 |
| 100 |
| y2 |
| 4 |
10-2
| 23 |
10-2
．| 23 |
分析：利用三角形的中位线，可得|OM|=
|PF′|，利用|MT|=|FT|-|FM|，可表示|MT|，再利用椭圆的定义，即可求得结论．
| 1 |
| 2 |
解答：解：由题意，设椭圆的右焦点为F′，连接PF′，OM，则|OM|=
|PF′|
∵|MT|=|FT|-|FM|=
-
|PF|=2
-
|PF|
∴|MO|-|MT|=
|PF′|- 2
+
|PF|=10-2
故答案为：10-2
| 1 |
| 2 |
∵|MT|=|FT|-|FM|=
| 100-4-4 |
| 1 |
| 2 |
| 23 |
| 1 |
| 2 |
∴|MO|-|MT|=
| 1 |
| 2 |
| 23 |
| 1 |
| 2 |
| 23 |
故答案为：10-2
| 23 |
点评：本题考查圆与圆锥曲线的综合，考查椭圆的定义，考查切线长的求解，属于中档题．
练习册系列答案
相关题目
)，B(－1，0)，C(1，0)，O为原点，从O点出发的光线先经AC上的点P1反射到边AB上，再由AB上的点P2反射回到BC边上的点P3停止，则光线OP1的斜率的范围为
，3
，2
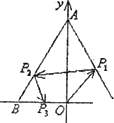
的左焦点F引圆
的切线FT交椭圆于点P，切点T位于F、P之间，M为线段FP的中点，M位于F、T之间，则
的值为_____________
的左焦点F引圆x2+y2=4的切线FT交椭圆于点P，切点T位于F、P之间，M为线段FP的中点，M位于F、T之间，则|MO|-|MT|的值为 ．
的左焦点F1引圆的切线F1T交椭圆于点P，切点T位于F1，P之间，M为线段F1P的中点，则|MO|-|MT|的值为（ ）。