题目内容
如图,已知椭圆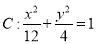 ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在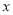 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线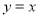 上.
上.

(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线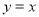 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.
(1)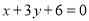 (2)详见解析
(2)详见解析
【解析】
试题分析:(1)两点确定一条直线,所以只需再确定A点坐标即可,这可利用A在椭圆上及AB中点在直线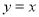 上联立方程组解得:A(
上联立方程组解得:A(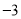 ,
, ),从而根据两点式求出直线AB的方程为
),从而根据两点式求出直线AB的方程为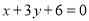 .
.
(2)本题涉及的条件为坐标,所以用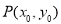 分别表示M点、N点坐标就是解题方法:由A,P,M三点共线,又点M在直线y=x上,解得M点的横坐标
分别表示M点、N点坐标就是解题方法:由A,P,M三点共线,又点M在直线y=x上,解得M点的横坐标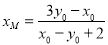 ,由B,P,N三点共线,点N在直线y=x上,,解得N点的横坐标
,由B,P,N三点共线,点N在直线y=x上,,解得N点的横坐标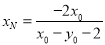 .所以OM·ON=
.所以OM·ON= =
=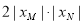 =2
=2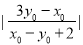
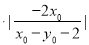
=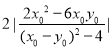 ,又
,又 ,所以OM·ON==
,所以OM·ON== =
= =
=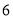 .
.
试题解析:【解析】
(1)设点E(m,m),由B(0,-2)得A(2m,2m+2).
代入椭圆方程得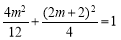 ,即
,即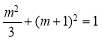 ,
,
解得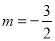 或
或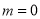 (舍). 3分
(舍). 3分
所以A( ,
, ),
),
故直线AB的方程为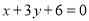 . 6分
. 6分
(2)设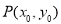 ,则
,则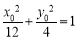 ,即
,即 .
.
设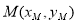 ,由A,P,M三点共线,即
,由A,P,M三点共线,即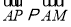 ,
,
∴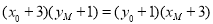 ,
,
又点M在直线y=x上,解得M点的横坐标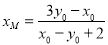 , 9分
, 9分
设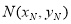 ,由B,P,N三点共线,即
,由B,P,N三点共线,即 ,
,
∴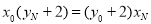 ,
,
点N在直线y=x上,,解得N点的横坐标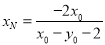 . 12分
. 12分
所以OM·ON= =
=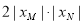 =2
=2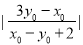
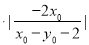
=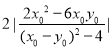 =
= =
= =
=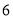 . 16分
. 16分
考点:直线与椭圆位置关系
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
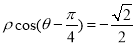 ,以极点为原点,极轴为x轴的非负半轴建立平面直角坐标系,曲线C2的参数方程为
,以极点为原点,极轴为x轴的非负半轴建立平面直角坐标系,曲线C2的参数方程为 ,求曲线C1与曲线C2交点的直角坐标
,求曲线C1与曲线C2交点的直角坐标 ,
, ,则
,则 .
.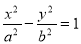 的右焦点到渐近线的距离是其到左顶点距离的一半,则双曲线的
的右焦点到渐近线的距离是其到左顶点距离的一半,则双曲线的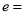 .
. 满足
满足

 (
( .
.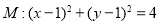 ,直线
,直线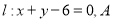 为直线
为直线 上一点,若圆
上一点,若圆 上存在两点
上存在两点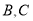 ,使得
,使得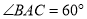 ,则点A的横坐标的取值范围是 .
,则点A的横坐标的取值范围是 . ,则输出的
,则输出的 的值为 .
的值为 .
 在点
在点 处的切线方程为 .
处的切线方程为 .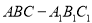 中,侧棱垂直于底面,点
中,侧棱垂直于底面,点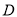 是
是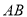 的中点.
的中点.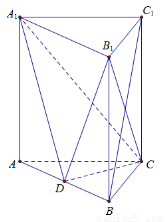
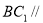 平面
平面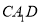 ;
;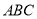 为边长为
为边长为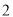 的正三角形,
的正三角形,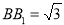 ,求三棱锥
,求三棱锥 的体积.
的体积.