题目内容
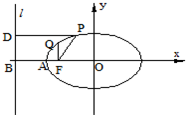 如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l(椭圆上的点到焦点的距离与到准线的距离之比等于离心率)交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则①
如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l(椭圆上的点到焦点的距离与到准线的距离之比等于离心率)交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则①| |PF| |
| |PD| |
| |QF| |
| |BF| |
| |FO| |
| |AO| |
| |AF| |
| |AB| |
分析:①由椭圆的第二定义可得:
=e;
②过点Q作QM⊥l于点M,则四边形BFQM是矩形,可得|QM|=|BF|,即可得出
=
=e;
③利用椭圆的性质可得
=
=e;
④利用椭圆的第二定义可得
=e.
| |PF| |
| |PD| |
②过点Q作QM⊥l于点M,则四边形BFQM是矩形,可得|QM|=|BF|,即可得出
| |QF| |
| |BF| |
| |QF| |
| |QM| |
③利用椭圆的性质可得
| |FO| |
| |AO| |
| c |
| a |
④利用椭圆的第二定义可得
| |AF| |
| |AB| |
解答:解:①由椭圆的第二定义可得:
=e;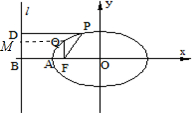
②过点Q作QM⊥l于点M,则四边形BFQM是矩形,可得|QM|=|BF|,∴
=
=e;
③
=
=e;
④由椭圆的第二定义可得
=e.
综上可知其中比值为椭圆的离心率为①②③④.
故选D.
| |PF| |
| |PD| |

②过点Q作QM⊥l于点M,则四边形BFQM是矩形,可得|QM|=|BF|,∴
| |QF| |
| |BF| |
| |QF| |
| |QM| |
③
| |FO| |
| |AO| |
| c |
| a |
④由椭圆的第二定义可得
| |AF| |
| |AB| |
综上可知其中比值为椭圆的离心率为①②③④.
故选D.
点评:本题考查了椭圆的第一和第二定义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则①
如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则① 如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则椭圆的离心率是①
如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则椭圆的离心率是①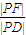 ;②
;②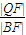 ;③
;③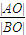 ;④
;④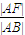 ;⑤
;⑤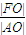 ,其中比值为椭圆的离心率的有( )
,其中比值为椭圆的离心率的有( )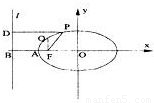
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ,其中比值为椭圆的离心率的有( )
,其中比值为椭圆的离心率的有( )