题目内容
已知数列{an},a1=1,前n项和为Sn,且点P(an,an+1)(n∈N*)在直线x-y+1=0上,则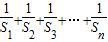 =( )
=( )A.
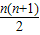
B.
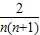
C.
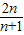
D.
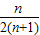
【答案】分析:由“P(an,an+1)(n∈N*)在直线x-y+1=0上”可得到数列的类型,再求其通项,求其前n项和,进而得到新数列的规律,选择合适的方法求新数列的和.
解答:解:∵点P(an,an+1)(n∈N*)在直线x-y+1=0上
∴an-an+1+1=0
∴数列{an}是以1为首项,以1为公差的等差数列.
∴an=n
∴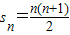
∴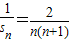 =
=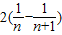
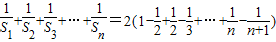 =
=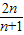
故选C
点评:本题主要是通过转化思想将解析几何问题转化为数列问题,来考查数列的通项公式及前n项和的求法.
解答:解:∵点P(an,an+1)(n∈N*)在直线x-y+1=0上
∴an-an+1+1=0
∴数列{an}是以1为首项,以1为公差的等差数列.
∴an=n
∴
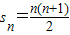
∴
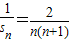 =
=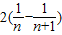
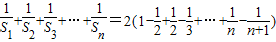 =
=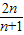
故选C
点评:本题主要是通过转化思想将解析几何问题转化为数列问题,来考查数列的通项公式及前n项和的求法.

练习册系列答案
相关题目