题目内容
设F为y2=6x的焦点，定点A（2，3），P为抛物线上的动点，则|FP|+|PA|的最小值为 ．
【答案】分析：设点P在准线上的射影为D，则根据抛物线的定义可知|PF|=|PD|进而把问题转化为求|PA|+|PD|取得最小，进而可推断出当D，P，A三点共线时|PA|+|PD|最小，答案可得．
解答：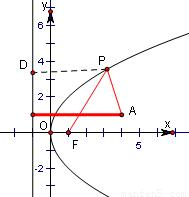
解：设点P在准线上的射影为D，则根据抛物线的定义可知|PF|=|PD|
∴要求|PA|+|PF|取得最小值，即求|PA|+|PD|取得最小
当D，P，A三点共线时|PA|+|PD|最小，为2-（-
）=
故答案为
．
点评：本题考查抛物线的简单性质，判断当D，P，A三点共线时|PA|+|PD|最小，是解题的关键．
解答：
解：设点P在准线上的射影为D，则根据抛物线的定义可知|PF|=|PD|∴要求|PA|+|PF|取得最小值，即求|PA|+|PD|取得最小
当D，P，A三点共线时|PA|+|PD|最小，为2-（-
）=故答案为
．点评：本题考查抛物线的简单性质，判断当D，P，A三点共线时|PA|+|PD|最小，是解题的关键．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目