题目内容
 (本题满分12分)如图,在正四棱锥
(本题满分12分)如图,在正四棱锥![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上. (Ⅰ)问点
上. (Ⅰ)问点![]() 在何处时,
在何处时,![]() ,并加以证明;(Ⅱ)当
,并加以证明;(Ⅱ)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离;(Ⅲ)求二面角
的距离;(Ⅲ)求二面角![]() 的大小.
的大小.
(Ⅰ) 见解析(Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
解析:
法一: (Ⅰ)当E为PC中点时,![]() .………2分
.………2分
连接AC,且![]() ,由于四边形ABCD为正方形,
,由于四边形ABCD为正方形,
∴O为AC的中点,又E为中点, ∴OE为△ACP的中位线,
∴OE为△ACP的中位线,
∴![]() ,又
,又![]() ,∴
,∴![]() ……4分
……4分
(Ⅱ) 点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]()
在正△DPC和正△BPC中,由于E为PC中点,
∴PC⊥DE,PC⊥BE ,又![]() ,
,
∴![]() ,PE即为所求,
,PE即为所求,![]()
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .………………………8分
.………………………8分
(Ⅲ)连接PO,则![]() ,∴
,∴![]() ,又BO⊥AC,
,又BO⊥AC,
∴![]() 点
点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
由三垂线定理得![]() .
.![]() 为二面角
为二面角![]() 的平面角. ………10分
的平面角. ………10分
在![]() 中,
中,![]() ,
,![]() .
.
又![]() ,
, ![]() 故二面角
故二面角![]() 的正弦值为
的正弦值为![]() .
.
故![]() . ………12分
. ………12分
解法二: (Ⅱ)作![]() ,依题意
,依题意![]() 是正方形
是正方形![]() 的中心,如图建立空间坐标系.
的中心,如图建立空间坐标系.
则![]() ,
,![]() ,
, ![]() ,
,![]()
![]() .
.
∴![]() ,
,![]() ,
,
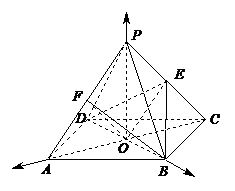
![]() ,
,![]()
设面![]() 的法向量为
的法向量为![]()
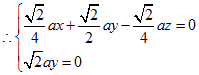
![]() , ……………… 6分
, ……………… 6分
点![]() 到平面
到平面![]() 的距离为
的距离为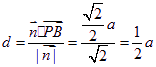 . ………………8分
. ………………8分
(Ⅲ)设二面角![]() 的平面角为
的平面角为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
, ![]() .………10分
.………10分
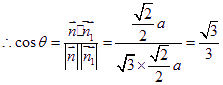 .
. ![]() ……………12分
……………12分

练习册系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
