题目内容
（2013•朝阳区二模）若
(x2+mx)dx=0，则实数m的值为（ ）
| ∫ | 1 0 |
分析：利用导数的运算法则可得(
+
)′=x2+mx，再利用微积分基本定理即可得出．
| x3 |
| 3 |
| mx2 |
| 2 |
解答：解：∵
(x2+mx)dx=(
+
)
=
+
，
令
+
=0，解得m=-
．
故选B．
| ∫ | 1 0 |
| x3 |
| 3 |
| mx2 |
| 2 |
| | | 1 0 |
| 1 |
| 3 |
| m |
| 2 |
令
| 1 |
| 3 |
| m |
| 2 |
| 2 |
| 3 |
故选B．
点评：熟练掌握导数的运算法则和微积分基本定理是解题的关键．
练习册系列答案
考前必练系列答案
相关题目
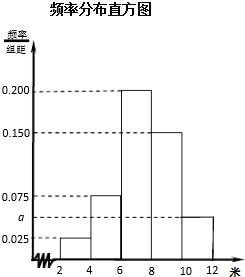（2013•朝阳区二模）为了解某市今年初二年级男生的身体素质状况，从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试．成绩低于6米为不合格，成绩在6至8米（含6米不含8米）的为及格，成绩在8米至12米（含8米和12米，假定该市初二学生掷实心球均不超过12米）为优秀．把获得的所有数据，分成[2，4），[4，6），[6，8），[8，10），[10，12]五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在10米到12米之间．