题目内容
设函数f（x）=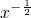
，则函数y=f（4x-3）的定义域是
- A.（-∞，+∞）
- B.
- C.
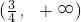
- D.
C
分析：由f（x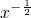）=的定义域为（0，+∞），知在函数y=f（4x-3）中，4x-3＞0，由此能求出函数y=f（4x-3）的定义域．
解答：∵f（x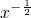）=的定义域为（0，+∞），
∴在函数y=f（4x-3）中，
4x-3＞0，
解得x＞
，
∴函数y=f（4x-3）的定义域是（，+∞）．
故选C．
点评：本题考查抽象函数的定义域，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．
分析：由f（x）=
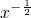的定义域为（0，+∞），知在函数y=f（4x-3）中，4x-3＞0，由此能求出函数y=f（4x-3）的定义域．解答：∵f（x）=
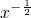的定义域为（0，+∞），∴在函数y=f（4x-3）中，
4x-3＞0，
解得x＞
，∴函数y=f（4x-3）的定义域是（
，+∞）．故选C．
点评：本题考查抽象函数的定义域，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
设函数f（x）=log2x，则f′（x）等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f（x）=2x，则如图所示的函数图象对应的函数是（ ）