题目内容
若△ABC的外接圆的圆心为O，半径为2，且
+
+
=0，则
•
=（ ）
| OA |
| OB |
| OC |
| OA |
| OB |
分析：由题意，
，
两向量的模已知，都是2，只需求出两向量的夹角即可求出两向量的数量积的值，由
+
+
=0，可得
+
=-
，结合向量加法的平行四边形法则可得出
，
两向量的夹角，数量积可求得
| OA |
| OB |
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
解答：解：由题意
+
+
=0，可得
+
=-
又△ABC的外接圆的圆心为O，半径为2
故
，
两向量的和向量的模是2，
由向量加法的平行四边形法则知，此时
，
两向量的和向量与两向量的夹角都是60°，
即
，
两向量的夹角为120°
∴
•
=2×2×cos120°=4×(-
)=-2
故选D
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
又△ABC的外接圆的圆心为O，半径为2
故
| OA |
| OB |
由向量加法的平行四边形法则知，此时
| OA |
| OB |
即
| OA |
| OB |
∴
| OA |
| OB |
| 1 |
| 2 |
故选D
点评：本题考查平面向量数量积的运算，考查了数量积的定义，向量加法法则，向量的夹角、相反向量等概念，解题的关键是根据题设条件
+
+
=0求出
，
两向量的夹角，向量是数与形结合的典范，做题时要注意与图形相对照，作出正确判断，本题考查了判断推理能力，属于向量基本题
| OA |
| OB |
| OC |
| OA |
| OB |
练习册系列答案
相关题目
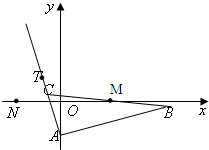已知△ABC的边AB边所在直线的方程为x-3y-6=0点B关于点M（2，0）的对称点为C，点T（-1，1）在AC边所在直线上且满足
=0，则
等于 ( )
B.0 C.1 D.
=0，则
·
=( )
B．0 C．1 D．