题目内容
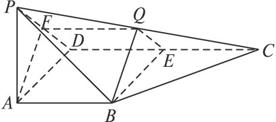
如图四边形ABCD是菱形，PA⊥平面ABCD，Q为PA的中点．
求证：（1）PC∥平面QBD；
（2）平面QBD⊥平面PAC．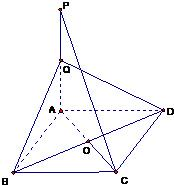
求证：（1）PC∥平面QBD；
（2）平面QBD⊥平面PAC．
证：设AC∩BD=O，连OQ．
（1）∵ABCD为菱形，∴O为AC中点，又Q为PA中点．
∴OQ∥PC （5分）
又PC?平面QBD，OQ?平面QBD，
∴PC∥平面QBD （7分）
（2）∵ABCD为菱形，∴BD⊥AC，（9分）
又∵PA⊥平面ABCD，BD?平面ABCD∴PA⊥BD （12分）
又PA∩AC=A∴BD⊥平面PAC又BD?平面QBD
∴平面QBD⊥平面PAC （14分）
（1）∵ABCD为菱形，∴O为AC中点，又Q为PA中点．
∴OQ∥PC （5分）
又PC?平面QBD，OQ?平面QBD，
∴PC∥平面QBD （7分）
（2）∵ABCD为菱形，∴BD⊥AC，（9分）
又∵PA⊥平面ABCD，BD?平面ABCD∴PA⊥BD （12分）
又PA∩AC=A∴BD⊥平面PAC又BD?平面QBD
∴平面QBD⊥平面PAC （14分）
练习册系列答案
相关题目
15、如图四边形ABCD是菱形，PA⊥平面ABCD，Q为PA的中点．
