题目内容
下列命题不正确的是( )
| A.若任意四点不共面,则其中任意三点必不共线 |
B.若直线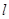 上有一点在平面 上有一点在平面 外,则 外,则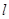 在平面 在平面 外 外 |
| C.若一个平面内的任一条直线都平行于另一个平面,则这两个平面平行 |
D.若直线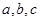 中, 中,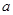 与 与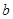 共面且 共面且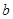 与 与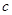 共面,则 共面,则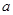 与 与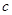 共面 共面 |
D.
解析试题分析:四点不共面则其中任意三点必不共线否则三点共线则四点一定共面,所以选项A是正确的. 若直线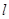 上有一点在平面
上有一点在平面 外,可能是直线与平行或直线与平面相交,所以直线在平面外正确.即选项B正确.选项C是平面平行的定义所以是对的.直线
外,可能是直线与平行或直线与平面相交,所以直线在平面外正确.即选项B正确.选项C是平面平行的定义所以是对的.直线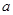 与
与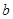 共面且
共面且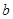 与
与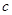 共面,直线
共面,直线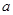 与
与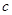 可以是异面的,本题可用正方体的棱来演示.所以选D.
可以是异面的,本题可用正方体的棱来演示.所以选D.
考点:1.直线与平面的位置关系.2.平面与平面的位置关系.3.直线与直线的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知直线 和平面
和平面 ,下列推论中错误的是( )
,下列推论中错误的是( )
A. | B. |
C. | D. |
设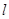 为直线,
为直线, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
下列命题中正确的个数是( )
(1)若直线 上有无数个点不在平面
上有无数个点不在平面 内,则
内,则 ∥
∥ .
.
(2)若直线 与平面
与平面 平行,则
平行,则 与平面
与平面 内的任意一条直线都平行.
内的任意一条直线都平行.
(3)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.
(4)若直线 与平面
与平面 平行,则
平行,则 与平面
与平面 内的任意一条直线都没有公共点.
内的任意一条直线都没有公共点.
| A.0 | B.1 | C. 2 | D.3 |
若P是两条异面直线l,m外的任意一点,则下列命题
①过点P有且只有一条直线与l,m都平行;
②过点P有且只有一条直线与l,m都垂直;
③过点P有且只有一条直线与l,m都相交;
④过点P有且只有一条直线与l,m都异面。
其中假命题的个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
在空间直角坐标系中,点 ,关于
,关于 轴对称的点的坐标是( )
轴对称的点的坐标是( )
A. | B. | C. | D. |
已知m,n是不同的直线, 是不重合的平面,下列命题正确的是( ):
是不重合的平面,下列命题正确的是( ):
A.若 |
B.若 |
C.若 |
D.若 |
设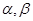 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题正确的是 ( )
是一条直线,以下命题正确的是 ( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则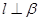 | D.若 ,则 ,则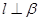 |

 B.
B. C.
C. D.0
D.0