题目内容
若直线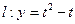 (
(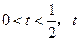 为常数)与函数
为常数)与函数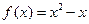 的图象以及y轴所围成的封闭图形的面积为
的图象以及y轴所围成的封闭图形的面积为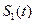 ,若直线l与函数
,若直线l与函数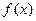 的图象所围成的封闭图形的面积为
的图象所围成的封闭图形的面积为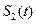 ,已知
,已知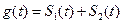 ,当
,当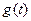 取最小值时,求t的值.
取最小值时,求t的值.
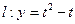 (
(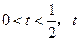 为常数)与函数
为常数)与函数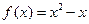 的图象以及y轴所围成的封闭图形的面积为
的图象以及y轴所围成的封闭图形的面积为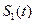 ,若直线l与函数
,若直线l与函数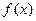 的图象所围成的封闭图形的面积为
的图象所围成的封闭图形的面积为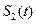 ,已知
,已知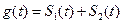 ,当
,当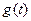 取最小值时,求t的值.
取最小值时,求t的值.
由 ,得交点坐标为
,得交点坐标为 和
和 ,
,
又∵ ,所以
,所以 ,
,
而函数 的顶点坐标为
的顶点坐标为 ,
,
由定积分的几何意义,得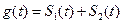
 .
.


 .
.
故 .
.
令 ,解得
,解得  或
或 (舍去).
(舍去).
当 时,
时, ,函数
,函数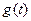 在区间
在区间 上单调递减;
上单调递减;
当 时,
时, ,函数
,函数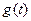 在区间
在区间 上单调递增.
上单调递增.
故当时,函数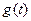 有最小值.
有最小值.
 ,得交点坐标为
,得交点坐标为 和
和 ,
,又∵
 ,所以
,所以 ,
,而函数
 的顶点坐标为
的顶点坐标为 ,
,由定积分的几何意义,得
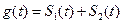
 .
.

 .
.故
 .
.令
 ,解得
,解得  或
或 (舍去).
(舍去).当
 时,
时, ,函数
,函数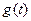 在区间
在区间 上单调递减;
上单调递减;当
 时,
时, ,函数
,函数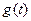 在区间
在区间 上单调递增.
上单调递增.故当时,函数
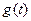 有最小值.
有最小值.
练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
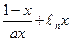 在[1,+∞
在[1,+∞ 上为增函数.
上为增函数.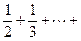
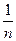
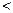
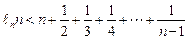 (n∈N*且n ≥ 2 )
(n∈N*且n ≥ 2 )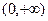 上的函数
上的函数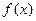 满足下面三个条件:
满足下面三个条件: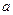 、
、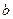 ,都有
,都有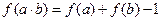 ; ②
; ②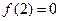 ;
;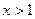 时,总有
时,总有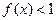 .
.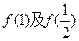 的值;
的值;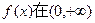 上是减函数.
上是减函数.
 的最大值
的最大值 的最小值为0,
的最小值为0,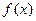 的最大值及此时x的集合。
的最大值及此时x的集合。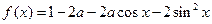 的最小值为
的最小值为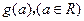
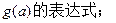 (2)若
(2)若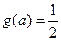 ,求
,求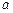 及此时
及此时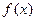 的最大值
的最大值 的单调递减区间是__________.
的单调递减区间是__________. 的最小值为 .
的最小值为 . 加4万元,每年销售环保建材的收入为50万元. 则该厂获取的纯利润达到最大值时是在第 年.
加4万元,每年销售环保建材的收入为50万元. 则该厂获取的纯利润达到最大值时是在第 年.