题目内容
如图，某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场，按照设计要求，休闲广场中间有两个完全相同的矩形绿化区域，周边及绿化区域之间是道路（图中阴影部分），道路的宽度均为2米．怎样设计矩形休闲广场的长和宽，才能使绿化区域的总面积最大？并求出其最大面积.
当休闲广场的长为
米，宽为
米时，绿化区域总面积最大值，最大面积为
平方米.
解析试题分析：先将休闲广场的长度设为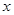
米，并将宽度也用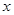进行表示，并将绿化区域的面积
表示成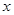的函数表达式，利用基本不等式来求出绿化区域面积的最大值，但是要注意基本不等式适用的三个条件.
试题解析：设休闲广场的长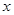为米，则宽为
米，绿化区域的总面积为平方米，
6分
，
8分
因为，所以
，
当且仅当
，即
时取等号 12分
此时取得最大值，最大值为.
答：当休闲广场的长为米，宽为米时，绿化区域总面积最大值，最大面积为平方米.
14分
考点：矩形的面积、基本不等式
练习册系列答案
相关题目
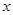（单位：cm）满足关系：
(
，
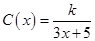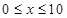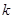为常数)，若不建隔热层，每年能源消耗费用为8万元．设
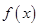为隔热层建造费用与20年的能源消耗费用之和．
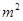的矩形蔬菜温室。在温室内，沿左．右两侧与后侧内墙各保留1
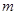宽的通道，沿前侧内墙保留3 
.
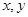都是正数，
，求
的最大值
，求
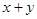的最小值．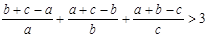
.
；
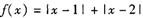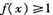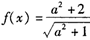成立，求x的取值范围.已知O为坐标原点，点A（1,0），若点M（x,y）为平面区域
内的一个动点，则
的最小值为( ).
| A．9 | B． | C． | D． |
+1的最小值 ；