题目内容
12.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60°,$\overrightarrow{AF}$=2$\overrightarrow{FB}$.(1)求椭圆C的离心率;
(2)如果|AB|=$\frac{15}{2}$,求椭圆C的方程.
分析 (1)点斜式设出直线l的方程,代入椭圆,得到A、B的纵坐标,再由$\overrightarrow{AF}$=2$\overrightarrow{FB}$,求出离心率;
(2)利用弦长公式和离心率的值,求出椭圆的长半轴、短半轴的值,从而写出标准方程.
解答 解:(1)设A(x1,y1),B(x2,y2),由题意知y1>0,y2<0.
直线l的方程为y=$\sqrt{3}$(x-c),其中c=$\sqrt{{a}^{2}-{b}^{2}}$.
联立$\left\{\begin{array}{l}{y=\sqrt{3}(x-c)}\\{{b}^{2}{x}^{2}+{a}^{2}{y}^{2}={a}^{2}{b}^{2}}\end{array}\right.$,得 (3a2+b2)y2+2$\sqrt{3}$b2cy-3b4=0.
解得y1=-$\frac{\sqrt{3}{b}^{2}(c+2a)}{3{a}^{2}+{b}^{2}}$,y2=-$\frac{\sqrt{3}{b}^{2}(c-2a)}{3{a}^{2}+{b}^{2}}$,
因为$\overrightarrow{AF}$=2$\overrightarrow{FB}$,所以-y1=2y2.
即-$\frac{\sqrt{3}{b}^{2}(c+2a)}{3{a}^{2}+{b}^{2}}$=2•$\frac{\sqrt{3}{b}^{2}(c-2a)}{3{a}^{2}+{b}^{2}}$,
解得离心率e=$\frac{c}{a}$=$\frac{2}{3}$;
另解:运用椭圆的第二定义,
设FB=m,AF=2m,
由三角形的相似性质,
可得$\frac{\frac{m}{2}}{\frac{m}{e}}$=$\frac{1}{3}$,
解得e=$\frac{2}{3}$;
(2)因为|AB|=$\sqrt{1+\frac{1}{3}}$•|y2-y1|,
∴$\frac{15}{2}$=$\sqrt{1+\frac{1}{3}}$•$\frac{4\sqrt{3}{b}^{2}a}{3{a}^{2}+{b}^{2}}$,
由e=$\frac{c}{a}$=$\frac{2}{3}$得b=$\frac{\sqrt{5}}{3}$a,所以$\frac{5}{4}$a=$\frac{15}{2}$,
解得a=6,b=2$\sqrt{5}$.
故椭圆C的方程为$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1.
点评 本题考查椭圆的性质和标准方程,以及直线和椭圆的位置关系,准确进行式子的变形和求值,是解题的难点,属于中档题.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案| A. | R<Q<P | B. | P<R<Q | C. | Q<R<P | D. | R<P<Q |
| A. | {x|x>0} | B. | {x|x>1} | C. | {x|0<x<1或x>1} | D. | ∅ |
 ,一条直径的两个端点恰好在两坐标轴上,求这个圆的方程.
,一条直径的两个端点恰好在两坐标轴上,求这个圆的方程. 的内角
的内角 、
、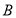 、
、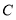 所对的边分别为
所对的边分别为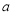 、
、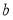 、
、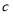 ,已知
,已知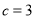 ,且
,且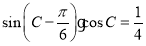 .
.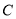 的大小;
的大小;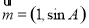 与
与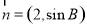 共线, 求
共线, 求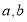 的值.
的值. ,则
,则 ( )
( ) B.
B. C.
C. D.
D.