题目内容
14.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点为F1,F2,点$P({\sqrt{2},\;1})$在C上,且PF2⊥x轴.(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线y=x+m与椭圆C交于不同的两点A,B,原点O在以AB为直径的圆外,求m的取值范围.
分析 (Ⅰ)依题意,点$P({\sqrt{2},\;1})$在C上,且PF2⊥x轴,可知$c=\sqrt{2}$,$\frac{2}{a^2}+\frac{1}{b^2}=1$,由此可得椭圆C的方程;
(Ⅱ)设A(x1,y1),B(x2,y2),则原点O在以线段AB为直径的圆外,等价于x1x2+y1y2>0,将直线与椭圆方程联立,利用韦达定理,可建立不等式,从而可求实数m的取值范围.
解答 解:(Ⅰ)由已知得$c=\sqrt{2}$,∴a2-b2=2①
又点$P({\sqrt{2},\;1})$在C上,∴$\frac{2}{a^2}+\frac{1}{b^2}=1$②(1分)
联立①②可得$\left\{\begin{array}{l}a=2\\ b=\sqrt{2}\end{array}\right.$ (3分)
故所求椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$. ( 4分)
(Ⅱ)设点A(x1y1),B(x2,y2),则$\overrightarrow{OA}=({{x_1},\;{y_1}})$,$\overrightarrow{OB}=({x_2},\;{y_2})$
由$\left\{\begin{array}{l}y=x+m\\ \frac{x^2}{4}+\frac{y^2}{2}=1\end{array}\right.$得3x2+4mx+2m2-4=0 (5分)
由△=16m2-12(2m2-4)=-8m2+48>0得$-\sqrt{6}<m<\sqrt{6}$${x_1}+{x_2}=-\frac{4m}{3}$,${x_1}{x_2}=\frac{{2{m^2}-4}}{3}$ (7分)
从而$\overrightarrow{OA}•\overrightarrow{OB}={x_1}{x_2}+{y_1}{y_2}={x_1}{x_2}+({x_1}+m)({x_2}+m)$=$2{x_1}{x_2}+m({x_1}+{x_2})+{m^2}$=$\frac{{4{m^2}-8}}{3}-\frac{{4{m^2}}}{3}+{m^2}$=$\frac{{-8+3{m^2}}}{3}$ (9分)
依题意有$\overrightarrow{OA}•\overrightarrow{OB}>0$,故$\frac{{-8+3{m^2}}}{3}>0$,
解得${m^2}>\frac{8}{3}$,即$m<-\frac{{2\sqrt{6}}}{3}$或$m>\frac{{2\sqrt{6}}}{3}$ (11分)
故m的取值范围是$({-\sqrt{6},\;-\frac{{2\sqrt{6}}}{3}})∪({\frac{{2\sqrt{6}}}{3},\;\sqrt{6}})$. (12分)
点评 本题考查椭圆的标准方程,考查向量知识的运用,考查韦达定理,解题的关键是联立方程,运用韦达定理解题.

| A. | (0,$\frac{π}{2}$) | B. | ($\frac{π}{2}$,π) | C. | (-$\frac{π}{2}$,-$\frac{π}{4}$) | D. | ($\frac{3π}{2}$,2π) |
| A. | 20 | B. | 18 | C. | 2 | D. | 以上均有可能 |
| A. | (0,±$\sqrt{5}$) | B. | (±$\sqrt{5}$,0) | C. | (0,±$\sqrt{13}$) | D. | (±$\sqrt{13}$,0) |
| A. | 过直线a可以作一个平面并且只可以作一个平面α与直线b平行 | |
| B. | 过直线a至多可以作一个平面α与直线b垂直 | |
| C. | 唯一存在一个平面α与直线a、b等距 | |
| D. | 可能存在平面α与直线a、b都垂直 |
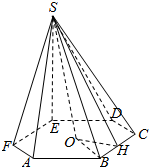 正六棱锥的底面周长为24,斜高SH与高SO所成的角为30°.
正六棱锥的底面周长为24,斜高SH与高SO所成的角为30°.