题目内容
已知直线l1过点A(-2,3),B(4,m),直线l2过点M(1,0),N(0,m-4),若l1⊥l2,则常数m的值是______.
∵直线l1过点A(-2,3),B(4,m),
∴直线l1的斜率k1=
=
,
同理直线l2过点M(1,0),N(0,m-4),
故直线l2的斜率k2=
,
因为l1⊥l2,所以k1•k2=
•
=-1,
即m2-7m+6=0,分解因式可得(m-1)(m-6)=0,
解得m=1或m=6,
故答案为:1或6
∴直线l1的斜率k1=
| m-3 |
| 4-(-2) |
| m-3 |
| 6 |
同理直线l2过点M(1,0),N(0,m-4),
故直线l2的斜率k2=
| m-4 |
| -1 |
因为l1⊥l2,所以k1•k2=
| m-3 |
| 6 |
| m-4 |
| -1 |
即m2-7m+6=0,分解因式可得(m-1)(m-6)=0,
解得m=1或m=6,
故答案为:1或6

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 上两点A(
上两点A( 及B(1,
及B(1, )所作的两条切线的夹角是
)所作的两条切线的夹角是



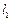 :
: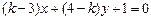 与直线
与直线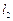 :
: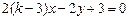 平行,则
平行,则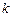 的值等于( )
的值等于( ) 时,两条直线
时,两条直线 、
、 的交点在 象限.
的交点在 象限.