题目内容
已知A、B、C是△ABC的三个内角,y=cotA+
.(1)若任意交换两个角的位置,y的值是否变化?试证明你的结论.
(2)求y的最小值.
解：(1)∵y=cotA+
=cotA+
=cotA+
=cotA+cotB+cotC,
∴任意交换两个角的位置,y的值不变化.
(2)∵cos(B-C)≤1,
∴y≥cotA+
=
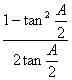+2tan
=
(cot
+3tan
)≥
=
.
故当A=B=C=
时,ymin=
.
讲评：本题的第(1)问是一道结论开放型题,y的表达式的表面不对称性显示了问题的有趣之处.第(2)问实际上是一道常见题:在△ABC中,求证:cotA+cotB+cotC≥
.
练习册系列答案
相关题目
β，则a∥b； ④若a与b异面，且a∥β，则b与β相交；