题目内容
已知直线y=x与函数 和图象交于点Q,P、M分别是直线y=x与函数
和图象交于点Q,P、M分别是直线y=x与函数 的图象上异于点Q的两点,若对于任意点M,PM≥PQ恒成立,则点P横坐标的取值范围是 .
的图象上异于点Q的两点,若对于任意点M,PM≥PQ恒成立,则点P横坐标的取值范围是 .
【答案】分析:由题意可得点Q(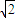 ,
,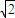 ),设M(a,
),设M(a, ),且 a>0,a≠
),且 a>0,a≠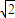 ,设P(b,b),则由PM≥PQ恒成立,可得
,设P(b,b),则由PM≥PQ恒成立,可得
b≤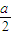 +
+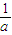 +
+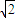 .由基本不等式可得
.由基本不等式可得 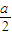 +
+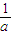 +
+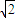 >2
>2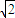 ,故 b≤2
,故 b≤2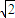 ,由此求得点P横坐标b的取值范围.
,由此求得点P横坐标b的取值范围.
解答:解:∵直线y=x与函数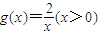 和图象交于点Q,∴点Q(
和图象交于点Q,∴点Q(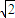 ,
,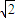 ).
).
由于 P、M分别是直线y=x与函数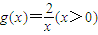 的图象上异于点Q的两点,
的图象上异于点Q的两点,
设M(a,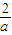 ),且 a>0,a≠
),且 a>0,a≠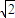 ,设P(b,b),则由PM≥PQ恒成立,
,设P(b,b),则由PM≥PQ恒成立,
可得 (b-a)2+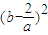 ≥
≥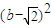 +
+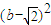 恒成立,化简可得 (2a+
恒成立,化简可得 (2a+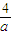 -4
-4 )b≤a2+
)b≤a2+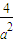 -4.
-4.
由于a>0,a≠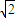 时,故(2a+
时,故(2a+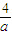 -4
-4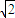 )>0,且 a2+
)>0,且 a2+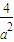 -4>0,由不等式可得
-4>0,由不等式可得
b≤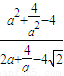 =
=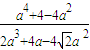 =
=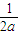 •
•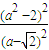 =
=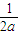 •
•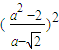
=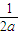 •
•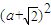 =
=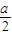 +
+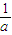 +
+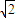 .
.
即 b≤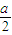 +
+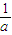 +
+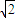 .
.
由a>0,a≠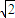 ,利用基本不等式可得
,利用基本不等式可得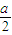 +
+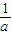 +
+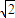 >2
>2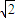 ,故 b≤2
,故 b≤2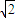 .
.
再由题意可得,b≠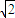 ,故点P横坐标b的取值范围是
,故点P横坐标b的取值范围是  ∪(
∪(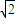 ,2
,2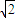 ].
].
故答案为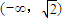 ∪(
∪( ,2
,2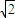 ].
].
点评:本题主要考查函数的恒成立问题,基本不等式的应用,式子变形是解题的难点和关键,属于中档题.
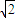 ,
,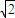 ),设M(a,
),设M(a, ),且 a>0,a≠
),且 a>0,a≠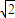 ,设P(b,b),则由PM≥PQ恒成立,可得
,设P(b,b),则由PM≥PQ恒成立,可得 b≤
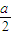 +
+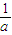 +
+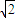 .由基本不等式可得
.由基本不等式可得 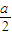 +
+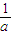 +
+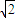 >2
>2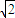 ,故 b≤2
,故 b≤2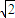 ,由此求得点P横坐标b的取值范围.
,由此求得点P横坐标b的取值范围.解答:解:∵直线y=x与函数
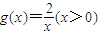 和图象交于点Q,∴点Q(
和图象交于点Q,∴点Q(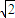 ,
,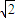 ).
).由于 P、M分别是直线y=x与函数
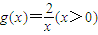 的图象上异于点Q的两点,
的图象上异于点Q的两点,设M(a,
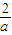 ),且 a>0,a≠
),且 a>0,a≠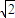 ,设P(b,b),则由PM≥PQ恒成立,
,设P(b,b),则由PM≥PQ恒成立,可得 (b-a)2+
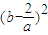 ≥
≥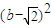 +
+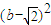 恒成立,化简可得 (2a+
恒成立,化简可得 (2a+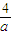 -4
-4 )b≤a2+
)b≤a2+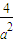 -4.
-4.由于a>0,a≠
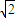 时,故(2a+
时,故(2a+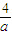 -4
-4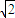 )>0,且 a2+
)>0,且 a2+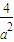 -4>0,由不等式可得
-4>0,由不等式可得b≤
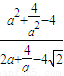 =
=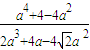 =
=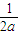 •
•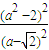 =
=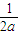 •
•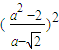
=
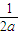 •
•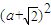 =
=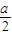 +
+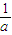 +
+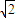 .
.即 b≤
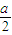 +
+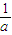 +
+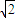 .
.由a>0,a≠
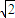 ,利用基本不等式可得
,利用基本不等式可得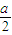 +
+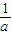 +
+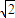 >2
>2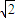 ,故 b≤2
,故 b≤2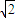 .
.再由题意可得,b≠
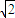 ,故点P横坐标b的取值范围是
,故点P横坐标b的取值范围是  ∪(
∪(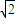 ,2
,2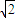 ].
].故答案为
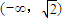 ∪(
∪( ,2
,2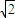 ].
].点评:本题主要考查函数的恒成立问题,基本不等式的应用,式子变形是解题的难点和关键,属于中档题.

练习册系列答案
相关题目
 和图象交于点Q,P、M分别是直线y=x与函数
和图象交于点Q,P、M分别是直线y=x与函数 的图象上异于点Q的两点,若对于任意点M,PM≥PQ恒成立,则点P横坐标的取值范围是 .
的图象上异于点Q的两点,若对于任意点M,PM≥PQ恒成立,则点P横坐标的取值范围是 .