题目内容
如图,曲线y=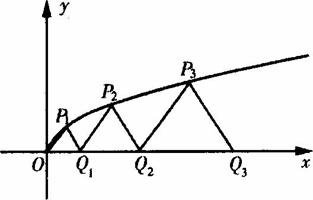
(Ⅰ)求a1的值;
(Ⅱ)求数列{an}的通项公式an;
(Ⅲ)设Sn为数列{an}的前n项和;若对于任意的实数λ∈[0,1],总存在自然数k,当n≥k时,3Sn-3n+2≥(1—λ)(3an-1)恒成立,求k的最小值.
解:(Ⅰ)由P1(![]() ,ti)(t>0),得
,ti)(t>0),得
![]() a1=|Q1Q0|=|OQ|=|OP1|=
a1=|Q1Q0|=|OQ|=|OP1|=![]()
(Ⅱ)设Pn(![]() ,tn),得直线PnQn-1的方程为:
,tn),得直线PnQn-1的方程为:
y-tn=![]() ,可得Qn-1(
,可得Qn-1(![]() )
)
直线PnQn的方程为y-tn=-(x![]() ),可得Qn(
),可得Qn(![]() ),
),
所以也有Qn-1(![]() ),得
),得![]() ,
,
由tn>0,得tn-tn-1=![]() 所以tn=t1+
所以tn=t1+![]() ,Qn(
,Qn(![]() n(n+1),0),
n(n+1),0),
Qn-1(![]() n(n-1),0) 故an=|QnQn-1|=
n(n-1),0) 故an=|QnQn-1|=![]() n
n
(Ⅲ)由已知对任意实数时λ∈[0,1]时n2-2n+2≥(1-λ)(2n—1)恒成立![]() 对任意实数λ∈[0,1]时,(2n-1)λ+n2-4n+3≥0恒成立则令f(λ)=(2n-1)λ+n2-4n+3,则f(λ)是关于λ的一次函数.
对任意实数λ∈[0,1]时,(2n-1)λ+n2-4n+3≥0恒成立则令f(λ)=(2n-1)λ+n2-4n+3,则f(λ)是关于λ的一次函数.![]() 对任意实数时λ∈[0,1]时n2-2n+2≥(1-λ)(2n-1)恒成立
对任意实数时λ∈[0,1]时n2-2n+2≥(1-λ)(2n-1)恒成立![]() 对任意实数,λ∈[0,1]时
对任意实数,λ∈[0,1]时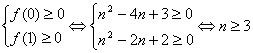 ,或n≤1 又∵n∈N* ∴k的最小值为3.
,或n≤1 又∵n∈N* ∴k的最小值为3.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
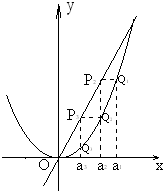 (2013•广州三模)如图,已知直线l:y=4x及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<4).从曲线C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
(2013•广州三模)如图,已知直线l:y=4x及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<4).从曲线C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.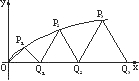 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y= 上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an= n(n+1).
n(n+1).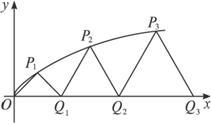
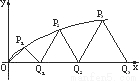 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y=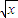 上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an= n(n+1).
n(n+1).