题目内容
已知椭圆 ,过右焦点F作不垂直于x轴的弦交椭圆于A、B两点,AB的垂直平分线交x轴于N,则|NF|:|AB|等于( )
,过右焦点F作不垂直于x轴的弦交椭圆于A、B两点,AB的垂直平分线交x轴于N,则|NF|:|AB|等于( )A.

B.

C.

D.

【答案】分析:由题可知此比例为定值,可取AB平行于x轴,依题意可求得AB=12,N与坐标原点重合,从而可得答案.
解答:解:依题意,|NF|:|AB|为定值,
∴取过右焦点F作平行于x轴的弦交椭圆于A、B两点,则|AB|=2a=12;
AB的垂直平分线交x轴于N,则N与坐标原点重合,
∴|NF|=|OF|=c=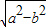 =
=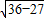 =3,
=3,
∴|NF|:|AB|=3:12= .
.
故选A.
点评:本题考查椭圆的简单性质,考查特殊位置法的灵活应用,灵活思维是关键,属于中档题.
解答:解:依题意,|NF|:|AB|为定值,
∴取过右焦点F作平行于x轴的弦交椭圆于A、B两点,则|AB|=2a=12;
AB的垂直平分线交x轴于N,则N与坐标原点重合,
∴|NF|=|OF|=c=
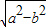 =
=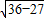 =3,
=3,∴|NF|:|AB|=3:12=
 .
.故选A.
点评:本题考查椭圆的简单性质,考查特殊位置法的灵活应用,灵活思维是关键,属于中档题.

练习册系列答案
相关题目
 ,过右焦点F作不垂直于
,过右焦点F作不垂直于 轴的弦交椭圆于A、B两点,AB的垂直平分线交
轴的弦交椭圆于A、B两点,AB的垂直平分线交 B.
B. C.
C. D.
D.
 ,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若 = .
= . ,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若 = .
= . ,过右焦点F斜率为
,过右焦点F斜率为 的直线与椭圆C交于A、B两点,若
的直线与椭圆C交于A、B两点,若 ,则椭圆C的离心率为( )
,则椭圆C的离心率为( )


