题目内容
若f(x),g(x)满足f'(x)=g'(x),则f(x)与g(x)满足
- A.f(x)=g(x)
- B.f(x)-g(x)为常数
- C.f(x)=g(x)=0
- D.f(x)+g(x)为常数
B
分析:先根据导数的运算法则将f′(x)=g′(x)转化为[f(x)-g(x)]′=0,然后由函数的求导法则可得答案.
解答:由f′(x)=g′(x),得f′(x)-g′(x)=0,
即[f(x)-g(x)]′=0,所以f(x)-g(x)=C(C为常数).
故选B.
点评:本题主要考查导数的运算法则,由f′(x)-g′(x)=0得到[f(x)-g(x)]′=0是解题关键,属基础题.
分析:先根据导数的运算法则将f′(x)=g′(x)转化为[f(x)-g(x)]′=0,然后由函数的求导法则可得答案.
解答:由f′(x)=g′(x),得f′(x)-g′(x)=0,
即[f(x)-g(x)]′=0,所以f(x)-g(x)=C(C为常数).
故选B.
点评:本题主要考查导数的运算法则,由f′(x)-g′(x)=0得到[f(x)-g(x)]′=0是解题关键,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
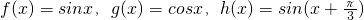 ;
;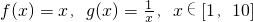 的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.
的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围. ;
; 的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.
的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.