题目内容
已知函数
，且存在
，使
。
（Ⅰ）证明：
是R上的单调增函数；
（Ⅱ）设
，
其中n=1，2，…
证明：
；
（Ⅲ）证明：
解析：（I）
∴
是R上的单调增函数.
（II）
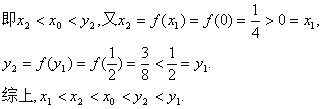
用数学归纳法证明如下：（1）当n=1时，上面已证明成立.
（2）假设当n=k （k≥1）时有 
当n=k+1时，由f(x)是单调增函数，有
由（1）和（2）对一切n=1，2，…，都有
（III）
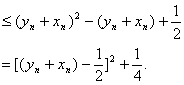
由（II）知 
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
，且存在
，使
．
，
，
，
，其中n=1，2，…
；
．
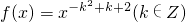，且f（2）＜f（3）
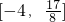．若存在，求出这个p的值；若不存在，说明理由．
，且函数y=f（x）的图象相邻两条对称轴之间的距离为
．
的值；
在区间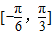
上单调递增，求实数k的取值范围；
内仅有一解，若存在，求出实数m的取值范围，若不存在，说明理由．
，且f（2）＜f（3）
．若存在，求出这个p的值；若不存在，说明理由．