题目内容
在四面体ABCD中，已知DA=DB=DC=1，且DA、DB、DC两两互相垂直，在该四面体表面上与点A距离为
的点形成一条曲线，则这条曲线的长度是（ ）
A．
B．
C．
D．
【答案】分析：先求出DG、DH的长，利用直角三角形中的边角关系求出∠DAG、∠DAH，得到∠CAG=∠HAB 的大小，弧长公式求得 
=
、以及 
、
的大小，这条曲线的长度是 
+
+
+
．
解答：
解：如图 勾股定理求出DG=
=
=DH，
tan∠DAG=
=
，∴∠DAG=
=∠DAH，
∴∠CAG=∠HAB=
-
=
，
∴由弧长公式得
=
=
×
=
，
=
×
=
，
∴这条曲线的长度是
+
+
+
=
+
+
+
×
=
．
故答案为
，
故选D．
点评：本题考查直角三角形中的边角关系，弧长公式的应用．本题中这条曲线是以A为球心，以
为半径的球与四面体表面的交线．
=、以及 、 的大小，这条曲线的长度是 +++．解答：
解：如图 勾股定理求出DG===DH，tan∠DAG=
=，∴∠DAG==∠DAH，∴∠CAG=∠HAB=
-=，∴由弧长公式得
==×=，=×=，∴这条曲线的长度是
+++=+++×=．故答案为
，故选D．
点评：本题考查直角三角形中的边角关系，弧长公式的应用．本题中这条曲线是以A为球心，以
为半径的球与四面体表面的交线． 
练习册系列答案
特高级教师点拨系列答案
相关题目
在四面体ABCD中，设AB=1，CD=2且AB⊥CD，若异面直线AB与CD间的距离为2，则四面体ABCD的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
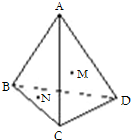在四面体ABCD中，M、N分别是面△ACD、△BCD的重心，则四面体的四个面中与MN平行的是
将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到四面体ABCD（如图2），则在四面体ABCD中，AD与BC的位置关系是（ ）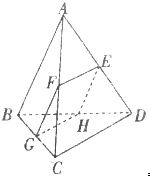
如图，在四面体ABCD中，截面EFGH平行于对棱AB和CD，且FG⊥GH，试问截面在什么位置时其截面面积最大．