题目内容
已知函数
（1）记
当
时，求函数
的单调区间；
（2）若对任意有意义的
，不等式
恒成立，求
的取值范围；
（3）求证：当
时，方程
有两个不等的实根
解：(1)当时，
……3分
当
时，
的单调减区间为
…………4分
当
时，
的单调减区间为
…………5分
(2) 等价于
，其中
…………6分
令
得
…………7分
当时，
当时，
…………10分
(3)设
，其中
等价于
此方程有且只有一个正根为
…………11分
且当
时，在
上单调递减；
当
时，在
上单调递增；
∴函数只有一个极值
…………12分
当时，关于在
递增，
…………13分
…………14分
………15分
当时，方程有两个不等的实根。………16分
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
，记数列{an}的前n项和为Sn，且有a1=f(1),当n≥2时，Sn－
(n2+5n－2).
，记数列{an}的前n项和为Sn,且有a1=f(1),当n≥2时，Sn-
(n2+5n-2).
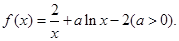
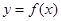在点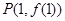
处的切线与直线
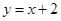垂直，求函数
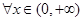都有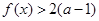
成立，试求实数a的取值范围；
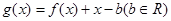，当a=1时，函数
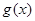在区间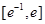
上有两个零点，求实数b的取值范围.
，有h(h(a))=a；
，使得h(m)=m，若m是函数h(x)的中介元，记
时h(x)的中介元为xn，且
，若对任意的
，都有Sn< 
,求
的取值范围；
时，函数y= h(x)的图像总在直线y=1-x的上方，求P的取值范围。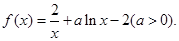
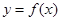在点
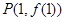处的切线与直线
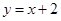垂直，求函数
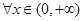都有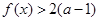
成立，试求实数a的取值范围；
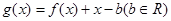，当a=1时，函数
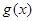在区间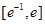
上有两个零点，求实数b的取值范围。