题目内容
如图，正方体ABCD-A1B1C1D1中，E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成角的余弦值是 ．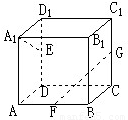
【答案】分析：以D为坐标原点，建立如图直角坐标系，可得出A1、E、G、F各点的坐标，从而得到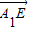
=（-2，0，-1），
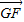=（2，-1，-1），再利用空间向量的夹角公式算出
、
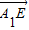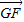夹角的余弦之值，取绝对值即可得到A1E与GF所成角的余弦值．
解答：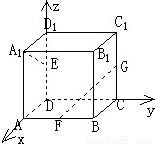
解：分别以DA、DC、DD1、为x、y、z轴建立如图坐标系，设正方体的棱长为2，则
A1（2，0，2），E（0，0，1），G（0，2，1），F（2，1，0）
∴
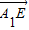=（-2，0，-1），
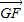=（2，-1，-1）
设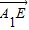
、
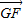的夹角为θ，则
cosθ=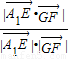
=
=
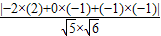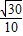
即异面直线A1E与GF所成角的余弦值是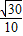
故答案为：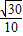
点评：本题在正方体中求两条异面直线所成的角，着重考查了正方体的性质和利用空间坐标系求异面直线所成角等知识点，属于基础题．
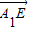=（-2，0，-1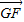），=（2，-1，-1），再利用空间向量的夹角公式算出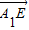、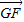夹角的余弦之值，取绝对值即可得到A1E与GF所成角的余弦值．解答：
解：分别以DA、DC、DD1、为x、y、z轴建立如图坐标系，设正方体的棱长为2，则A1（2，0，2），E（0，0，1），G（0，2，1），F（2，1，0）
∴
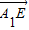=（-2，0，-1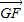），=（2，-1，-1）设
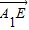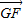、的夹角为θ，则cosθ=
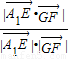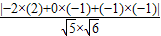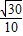
==即异面直线A1E与GF所成角的余弦值是
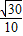
故答案为：
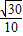
点评：本题在正方体中求两条异面直线所成的角，着重考查了正方体的性质和利用空间坐标系求异面直线所成角等知识点，属于基础题．
练习册系列答案
相关题目
如图，正方体ABCD-A1B1C1D1中，E，F分别为BB1和A1D1的中点．证明：向量
如图，正方体ABCD-A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．
如图，正方体ABCD-A1B1C1D1中，若E、F、G分别为棱BC、C1C、B1C1的中点，O1、O2分别为四边形ADD1A1、A1B1C1D1的中心，则下列各组中的四个点不在同一个平面上的是（ ）
如图，正方体ABCD-A1B1C1D1中，E、F、G、H分别是所在棱的三等分点，且