题目内容
设双曲线 的实轴的两个端点为A1,A2,线段A1A2被抛物线x2=py(p>0)的焦点分成5:3的两段,若此双曲线的离心率为
的实轴的两个端点为A1,A2,线段A1A2被抛物线x2=py(p>0)的焦点分成5:3的两段,若此双曲线的离心率为 ,则b:P等于
,则b:P等于
- A.3:2
- B.3:4
- C.4:3
- D.6:5
B
分析:由题意结合图形分析知 ,即a=p; 据离心率得到
,即a=p; 据离心率得到  ,求得
,求得  .
.
解答:抛物线的焦点 ,由题意结合图形分析知
,由题意结合图形分析知 ,即a=p;
,即a=p;
又由曲线的离心率 ,即
,即  ,
,
16a2+16b2=25a2,得16b2=9a2,即 ,
,
故选B.
点评:本题考查双曲线、抛物线的标准方程和简单性质,求得 ,即a=p,是解题的关键.
,即a=p,是解题的关键.
分析:由题意结合图形分析知
 ,即a=p; 据离心率得到
,即a=p; 据离心率得到  ,求得
,求得  .
.解答:抛物线的焦点
 ,由题意结合图形分析知
,由题意结合图形分析知 ,即a=p;
,即a=p; 又由曲线的离心率
 ,即
,即  ,
,16a2+16b2=25a2,得16b2=9a2,即
 ,
,故选B.
点评:本题考查双曲线、抛物线的标准方程和简单性质,求得
 ,即a=p,是解题的关键.
,即a=p,是解题的关键. 
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 的实轴两个端点,P1P2是双曲线的垂直于
的实轴两个端点,P1P2是双曲线的垂直于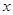 轴的弦,
轴的弦, 的方程;
的方程; 与
与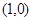 ,求证:
,求证: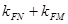 为定值;
为定值; 的实轴的两个端点为A1,A2,线段A1A2被抛物线x2=py(p>0)的焦点分成5:3的两段,若此双曲线的离心率为
的实轴的两个端点为A1,A2,线段A1A2被抛物线x2=py(p>0)的焦点分成5:3的两段,若此双曲线的离心率为 ,则b:P等于( )
,则b:P等于( ) 的实轴的两个端点为A1,A2,线段A1A2被抛物线x2=py(p>0)的焦点分成5:3的两段,若此双曲线的离心率为
的实轴的两个端点为A1,A2,线段A1A2被抛物线x2=py(p>0)的焦点分成5:3的两段,若此双曲线的离心率为 ,则b:P等于( )
,则b:P等于( )