题目内容

已知数列{an}，如果a1，a2-a1，a3-a2，…，an-an-1，是首项为1，公比为2的等比数列，那么an=（　　）
A．2n+1-1B．2n-1C．2n-1D．2n+1
由题意可得，an-an-1=2n-1
∴a2-a1=2
a3-a2=22
…
an-an-1=2n-1
以上n-1个式子相加可得，an-a1=2+22+…+2n-1=
2(1-2n-1)
1-2
=2n-2
∴an=2n-1
故选B
练习册系列答案
相关题目
已知数列{an}满足如图所示的程序框图．
（I）写出数列{an}的一个递推关系式；并求数列{an}的通项公式
（Ⅱ）设数列{an}的前n项和Sn，证明不等式Sn+1≤4Sn，对任意n∈N*皆成立．
已知数列{an}满足如图所示的流程图
（Ⅰ）写出数列{an}的一个递推关系式；
（Ⅱ）证明：{an+1-3an}是等比数列；并求出{an}的通项公式；
（Ⅲ）求数列{n(an+3n-1)}的前n项和Tn．
已知数列{an}满足如图所示的程序框图．
（Ⅰ）写出当n=1，2，3时输出的结果；
（Ⅱ）写出数列{an}的一个递推关系式，并证明：{an+1-3an}是等比数列；
（Ⅲ）求{an}的通项公式及前n项和Sn．
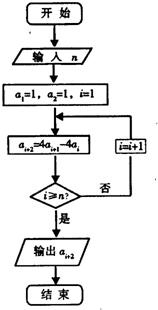精英家教网已知数列{an}满足如图所示的程序框图．
（I）写出数列{an}的一个递推关系式；
（II）证明：{an+1-2an}是等比数列；
（III）证明{
an2n
}是等差数列，并求{an}的通项公式．
已知数列{an}满足如图所示的程序框图．
（I）写出数列{an}的一个递推关系式；
（II）证明：{an+1-2an}是等比数列；
（III）证明是等差数列，并求{an}的通项公式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网