题目内容
如图，在
中，∠A是直角，
，有一个椭圆以
为一个焦点，另一个焦点Q在AB上，且椭圆经过点A、B.
（1）求椭圆的离心率；
（2）若以PQ所在直线为
轴，线段PQ的垂直平分线为
轴建立直角坐标系，求椭圆的方程；
（3）在（2）的条件下，若经过点Q的直线
将的面积分为相等的两部分，求直线的方程.
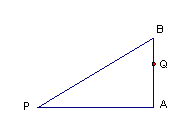
（1）因为椭圆以P为一个焦点，另一个焦点Q在AB上，且椭圆经过点A、B，
所以由椭圆的定义知
，
因此
，解得
.
于是椭圆的长轴长
，焦距
，
故椭圆的离心率
.
（2）依题意，可设椭圆方程为
，
由（1）知，
，∴
，∴椭圆方程为
.
（3）依题意，设直线
的方程为
，
设直线与PA相交于点C，则
，故
，从而
.
设
，由
，得
，解得
.
设
，由，得
，解得
.
∴
，∴直线的方程为
.
练习册系列答案
阅读快车系列答案
相关题目
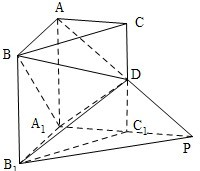如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1=1，D是棱CC1上的一点，P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA1
如图，在等腰梯形ABCD中，M，N分别是AB，CD的中点，沿MN将MNCB折起至MNC1B1，使它与MNDA成直二面角．已知AB=2CD=4MN，给出下列四个等式：
如图，在三棱锥A-BOC中，AO⊥面BOC，二面角B-AO-C是直二面角，OB=OC，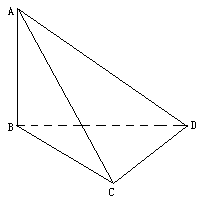
，AD与平面ABC所成的角为
，求二面角B—AD—C的余弦值；