题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,试证明:
,试证明:![]() .
.
【答案】(1)![]() 在区间
在区间![]() 上为减函数;
上为减函数;![]() 在区间
在区间![]() 上为增函数.(2)证明见解析
上为增函数.(2)证明见解析
【解析】
(1)对函数进行求导得![]() ,再对
,再对![]() 分成
分成![]() 和
和![]() 两种情况讨论,从而得到函数的单调性;
两种情况讨论,从而得到函数的单调性;
(2)将不等式等价于![]() ,再对
,再对![]() 分成
分成![]() 和
和![]() 两种情况讨论.
两种情况讨论.
(1)由 ![]()
![]() 知:
知:
(i)若![]() ,
,![]() ,∴
,∴ ![]() 在区间
在区间![]() 上为增函数.
上为增函数.
(ii)若![]() ,
,
∴当![]()
![]() 时,有
时,有![]() ,∴
,∴ ![]() 在区间
在区间![]() 上为减函数.
上为减函数.
当![]()
![]() 时,有
时,有![]() ,∴
,∴ ![]() 在区间
在区间![]() 上为增函数.
上为增函数.
综上:当![]() 时,
时,![]() 在区间
在区间![]() 上为增函数;
上为增函数;
当![]() 时,
时,![]() 在区间
在区间![]() 上为减函数;
上为减函数;![]() 在区间
在区间![]() 上为增函数.
上为增函数.
(2)若![]() ,则
,则![]()
要证![]() ,只需证
,只需证![]() ,
,
即证:![]() .
.
(i)当![]() 时,
时,![]() ,而
,而![]()
∴此时![]() 成立.
成立.
(ii)当![]() 时,令
时,令![]() ,
,![]() ,
,
∵ ![]() ,
,
设![]() ,
,
则 ![]()
![]()
![]() ,∴
,∴![]()
∴当![]() 时,
时,![]() 单调递增,∴
单调递增,∴![]() ,即
,即![]()
∴![]() 在
在![]() 单调递增,∴
单调递增,∴![]()
即![]() ,即
,即![]() ,
,
∴![]()
综上:当![]() 时,有
时,有![]() 成立.
成立.

练习册系列答案
相关题目
【题目】哈三中团委组织了“古典诗词”的知识竞赛,从参加考试的学生中抽出60名学生(男女各30名),将其成绩分成六组![]() ,
,![]() ,…,
,…,![]() ,其部分频率分布直方图如图所示.
,其部分频率分布直方图如图所示.
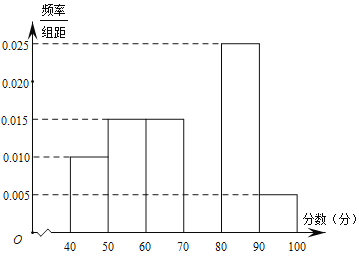
(Ⅰ)求成绩在![]() 的频率,补全这个频率分布直方图,并估计这次考试的众数和中位数;
的频率,补全这个频率分布直方图,并估计这次考试的众数和中位数;
(Ⅱ)从成绩在![]() 和
和![]() 的学生中选两人,求他们在同一分数段的概率;
的学生中选两人,求他们在同一分数段的概率;
(Ⅲ)我们规定学生成绩大于等于80分时为优秀,经统计男生优秀人数为4人,补全下面表格,并判断是否有99%的把握认为成绩是否优秀与性别有关?
优秀 | 非优秀 | 合计 | |
男 | 4 | 30 | |
女 | 30 | ||
合计 | 60 |
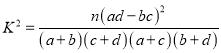
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |