题目内容
(本小题满分12分)设双曲线 的两个焦点分别为
的两个焦点分别为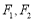 ,离心率为2.
,离心率为2.
(Ⅰ)求此双曲线的渐近线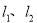 的方程;
的方程;
(Ⅱ)若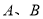 分别为
分别为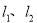 上的点,且2|AB|=5|F1F2|,求线段
上的点,且2|AB|=5|F1F2|,求线段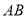 的中点M的轨迹方程,并说明轨迹是什么曲线。
的中点M的轨迹方程,并说明轨迹是什么曲线。
(Ⅰ)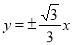 ,(Ⅱ)
,(Ⅱ) 的轨迹方程为
的轨迹方程为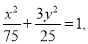 则
则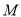 的轨迹是中心在原点,焦点在
的轨迹是中心在原点,焦点在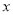 轴上长轴长为
轴上长轴长为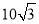 ,短轴长为
,短轴长为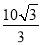 的椭圆.
的椭圆.
【解析】
试题分析:由离心率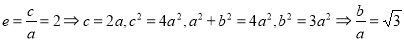 ,得出渐近线方程;第二步设而不求,先设出
,得出渐近线方程;第二步设而不求,先设出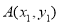 ,
,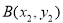 ,
,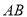 的中点
的中点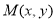 ,利用已知条件
,利用已知条件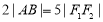 ,得出相应的关系,再根据点
,得出相应的关系,再根据点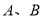 分别为
分别为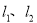 上的点,坐标满足直线方程
上的点,坐标满足直线方程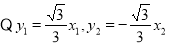 ,两式相加得
,两式相加得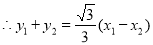 ,两式相减得:
,两式相减得: ,把
,把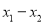 和
和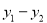 代入
代入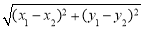 =10,另外利用中点坐标公式
=10,另外利用中点坐标公式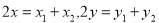 ,求出点
,求出点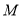 的轨迹方程;
的轨迹方程;
试题解析:(Ⅰ)由 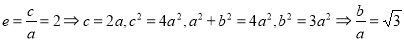 ,双曲渐近线方程为
,双曲渐近线方程为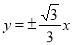 ;
;
(Ⅱ)设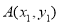 ,
,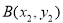 ,
,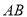 的中点
的中点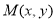
∵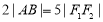 ∴
∴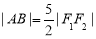
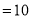 ,∴
,∴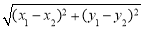 =10,又
=10,又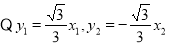 ,两式相加
,两式相加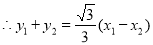 ,两式相减:
,两式相减: ,则
,则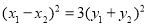 ,
,
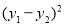
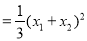 ,
,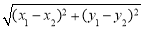
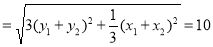 则根据中点坐标公式:
则根据中点坐标公式: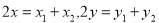 ,∴
,∴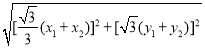
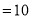 ,则
,则 的轨迹方程为
的轨迹方程为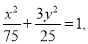
则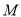 的轨迹是中心在原点,焦点在
的轨迹是中心在原点,焦点在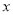 轴上长轴长为
轴上长轴长为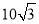 ,短轴长为
,短轴长为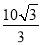 的椭圆.
的椭圆.
考点:1.双曲线的离心率与渐近线方程;2.求动点轨迹方程;

练习册系列答案
相关题目
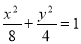 有相同的焦点,实半轴长为
有相同的焦点,实半轴长为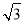 .
.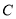 的方程;
的方程;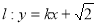 与双曲线
与双曲线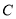 有两个不同的交点
有两个不同的交点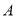 和
和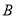 ,且
,且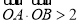 (其中
(其中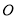 为原点),求
为原点),求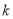 的取值范围.
的取值范围. 有公共焦点,且离心率
有公共焦点,且离心率 的双曲线方程为( )
的双曲线方程为( ) B.
B.
 D.
D.
 焦点的直线交抛物线于
焦点的直线交抛物线于 ,
, 两点,若
两点,若 ,则
,则 的中点到
的中点到 轴的距离等
轴的距离等 B.
B.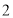 C.
C.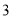 D.
D.
 ,则
,则 的值为( )
的值为( ) D.
D.
 是等差数列,数列
是等差数列,数列 是等比数列,则
是等比数列,则 的值为 _______ .
的值为 _______ .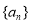 是等比数列,其前n项和为
是等比数列,其前n项和为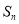 ,若
,若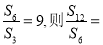 ( )
( ) +
+ ,
, ∈(0,π),则tan
∈(0,π),则tan 、
、 满足条件
满足条件 ,则
,则 的最小值为___________;
的最小值为___________;