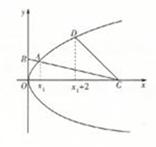
题目内容
已知抛物线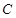 的顶点为原点,其焦点
的顶点为原点,其焦点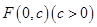 到直线
到直线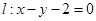 的距离为
的距离为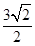 .设
.设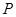 为直线
为直线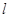 上的点,过点
上的点,过点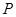 作抛物线
作抛物线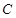 的两条切线
的两条切线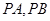 ,其中
,其中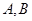 为切点.
为切点.
(Ⅰ)求抛物线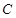 的方程;
的方程;
(Ⅱ)当点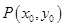 为直线
为直线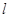 上的定点时,求直线
上的定点时,求直线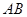 的方程;
的方程;
(Ⅲ)当点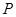 在直线
在直线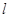 上移动时,求
上移动时,求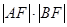 的最小值.
的最小值.
(1) 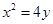 (2)
(2)  (3)
(3) 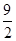
解析试题分析: (1)利用点到直线的距离公式直接求解C的值,便可确定抛物线方程;(2)利用求导的思路确定抛物线的两条切线,借助均过点P,得到直线方程;(3)通过直线与抛物线联立,借助韦达定理和抛物线定义将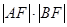 进行转化处理,通过参数的消减得到函数关系式
进行转化处理,通过参数的消减得到函数关系式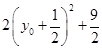 是解题的关键,然后利用二次函数求最值,需注意变量的范围.
是解题的关键,然后利用二次函数求最值,需注意变量的范围.
试题解析:(1)依题意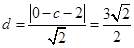 ,解得
,解得 (负根舍去) (2分)
(负根舍去) (2分)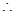 抛物线
抛物线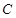 的方程为
的方程为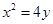 ; (4分)
; (4分)
(2)设点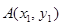 ,
,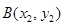 ,
, ,由
,由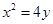 ,即
,即 得
得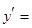
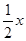 .
.
∴抛物线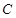 在点
在点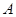 处的切线
处的切线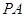 的方程为
的方程为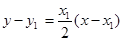 ,即
,即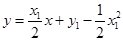 . (5分)
. (5分)
∵ , ∴
, ∴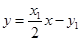 . ∵点
. ∵点 在切线
在切线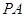 上, ∴
上, ∴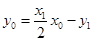 . ①
. ①
同理, 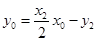 . ② (6分)
. ② (6分)
综合①、②得,点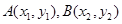 的坐标都满足方程
的坐标都满足方程 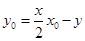 . (7分)
. (7分)
∵经过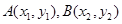 两点的直线是唯一的,∴直线
两点的直线是唯一的,∴直线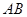 的方程为
的方程为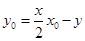 ,即
,即 ; (8分)
; (8分)
(3)由抛物线的定义可知 , (9分)
, (9分)
所以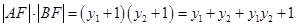 联立
联立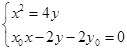 ,消去
,消去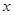 得
得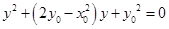 ,
,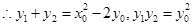 (10分)
(10分)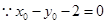
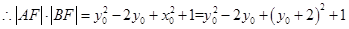
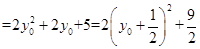 (11分)
(11分)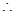 当
当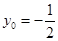 时,
时,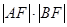 取得最小值为
取得最小值为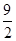 (12分)
(12分)
考点:抛物线的方程、定义、切线方程以及直线与抛物线的位置关系.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
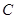 的中心在原点
的中心在原点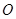 ,离心率
,离心率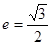 ,右焦点为
,右焦点为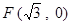 .
.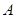 ,在椭圆
,在椭圆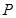 ,使得向量
,使得向量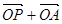 与
与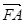 共线?若存在,求直线
共线?若存在,求直线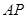 的方程;若不存在,简要说明理由.
的方程;若不存在,简要说明理由.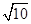 时,求k的值.
时,求k的值. 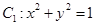 在矩阵
在矩阵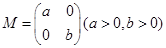 的变换作用下得到曲线
的变换作用下得到曲线 .
.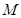 ;
;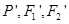 ,求以
,求以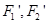 为焦点且过
为焦点且过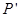 点的双曲线的标准方程。
点的双曲线的标准方程。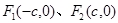 分别是椭圆C:
分别是椭圆C: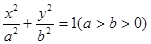 的左、右焦点,过点
的左、右焦点,过点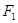 作
作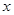 轴的垂线,交椭圆
轴的垂线,交椭圆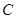 的上半部分于点
的上半部分于点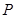 ,过点
,过点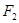 作
作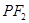 的垂线交直线
的垂线交直线 于点
于点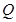 .
.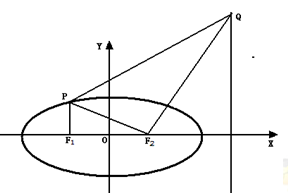
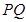 与椭圆
与椭圆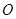 ,半径为
,半径为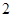 .从这个圆上任意一点
.从这个圆上任意一点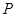 向
向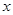 轴作垂线
轴作垂线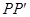 ,
,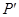 为垂足.
为垂足.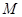 的轨迹方程;
的轨迹方程; 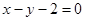 与
与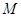 的轨迹相交于
的轨迹相交于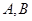 两点,求
两点,求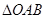 的面积
的面积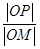 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.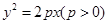 的准线过椭圆N:
的准线过椭圆N: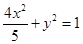 的左焦点,以坐标原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的部分以及y轴的正半轴相交于点A与点B,直线AB与x轴相交于点C.
的左焦点,以坐标原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的部分以及y轴的正半轴相交于点A与点B,直线AB与x轴相交于点C.